题目内容
设 ,则
,则 的解集为
的解集为
A. | B. | C. | D. |
C
解析试题分析: 因为 ,那么可知
,那么可知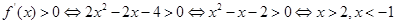 ,因为定义域x>0,故不等式的解集为x>2,选C.
,因为定义域x>0,故不等式的解集为x>2,选C.
考点:本题主要考查了超越不等式的求解的运用。
点评:解决该试题的关键是利用导数的运算得到导函数,然后求解关于一元二次不等式的解集的问题,同时要注意分式化为整式不等式的等价变形。

练习册系列答案
相关题目
已知函数 ,且
,且 .则( )
.则( )
A. | B. |
C. | D. |
已知函数 ,
, ,
, ,
, ,
,
( )
A. | B. | C. | D. |
已知二次函数 的导数为
的导数为 ,
, ,对于任意实数
,对于任意实数 都有
都有 ,则
,则 的最小值为( )
的最小值为( )
| A.3 | B. | C.2 | D. |
若 ,则满足不等式
,则满足不等式 的x的范围是( )
的x的范围是( )
A.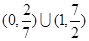 | B.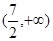 |
C. | D. |
已知函数 ,若
,若 互不相等,且
互不相等,且 ,
,
则 的取值范围是( )
的取值范围是( )
| A.(1,10) | B.(5,6) | C.(10,12) | D.(20,24) |
函数 的值域为( )
的值域为( )
A. | B. | C. | D. |
设f (x)是奇函数,且在(0,+∞)上是增函数,又f (-3)=0,则x·f (x)<0的解集为
| A.{x∣-3<x<0或x>3} |
| B.{x∣x<-3或0<x<3} |
| C.{x∣x<-3或x>3} |
| D.{x∣-3<x<0或0<x<3} |
设幂函数 的图像经过点
的图像经过点 ,设
,设 ,则
,则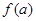 与
与 的大小关系是( )
的大小关系是( )
A. | B. | C. | D.不能确定 |