Question

已知圆O的方程是x²＋y²＝9.求过点A(1,2)，所作圆的弦的中点P的轨迹方程．

Answer 1

设过点A的弦所在的直线方程为y－2＝k(x－1)(k存在时)，且设P点坐标为(x，y)，

依题意，消去y，得

(1＋k²)x²＋2k(2－k)x＋k²－4k－5＝0.

∴x₁＋x₂＝，

∴x＝＝，

∴y＝＋2－k＝，

∴.

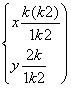消去参数k得P点的轨迹方程是x²＋y²－x－2y＝0.当k不存在时，中点P(1,0)的坐标也适合上述方程．

故P点的轨迹为以点为圆心，为半径的圆．