题目内容
等差数列中,若a3+a4+a5+a6+a7+a8+a9=420,则a2+a10=( )
| A.100 | B.120 | C.140 | D. 160 |
B
解析试题分析:根据等差数列的性质可知,由a3+a4+a5+a6+a7+a8+a9=(a3+a9)+(a4+a8)+(a5+a7)+a6=7a6=420,得到a6=60,则a2+a12=2a6=120.故选B
考点:本题主要考查了学生灵活运用等差数列的性质化简求值,是一道基础题.学生化简已知条件时注意项数之和等于10的两项结合
点评:解决该试题的关键是根据等差数列的性质可知,项数之和相等的两项之和相等,化简已知的等式即可求出a5的值,然后把所求的式子也利用等差数列的性质化简后,将a5的值代入即可求出值.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
等差数列 中,若
中,若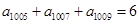 ,则该数列前2013项的和为
,则该数列前2013项的和为
A.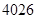 | B.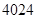 | C.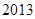 | D.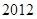 |
等差数列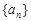 中,a3="7," a9=19,则a5= ( )
中,a3="7," a9=19,则a5= ( )
| A.10 | B.11 | C.12 | D.13 |
设等差数列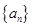 的前
的前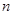 项和为
项和为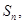
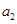 、
、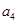 是方程
是方程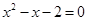 的两个根,则
的两个根,则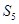 等于( )
等于( )
A.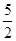 | B.5 | C.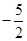 | D.-5 |
已知数列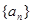 为等差数列,若
为等差数列,若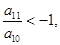 且它们的前
且它们的前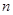 项和
项和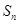 有最大值,则使得
有最大值,则使得 的
的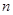 的最大值为( )
的最大值为( )
| A.11 | B.19 | C.20 | D.21 |
已知等差数列 的前
的前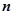 项和为
项和为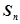 ,且满足
,且满足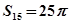 ,则
,则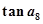 的值是( )
的值是( )
A. | B.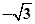 | C.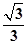 | D.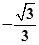 |
在各项均为正数的等比数列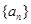 中,
中,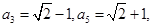 则
则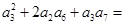 ( )
( )
| A.4 | B.6 | C.8 | D.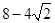 |
如果等差数列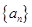 中,
中, ,那么
,那么
| A.14 | B.21 | C.28 | D.35 |
等差数列{an}中,若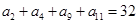 ,则
,则 ( )
( )
| A.9 | B.12 | C.15 | D.16 |