题目内容
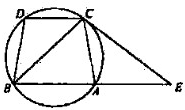 如图,ABCD是圆的内接四边形,AB∥CD,过C点的圆的切线与BA的延长线交于E点,
如图,ABCD是圆的内接四边形,AB∥CD,过C点的圆的切线与BA的延长线交于E点,证明:
(Ⅰ)∠DBC=∠AEC;
(Ⅱ)BC2=BE•CD.
分析:(Ⅰ)根据圆的内接四边形的对角互补可得∠CAE=∠BDC,根据弦切角等于弧所对的圆周角得到∠ACE=∠ABC,以及内错角相等可得∠DCB=∠ABC,从而得到△BDC相似于△EAC,从而得到结论;
(II)由(I)可得到∠BCE=∠BDC,而∠EBC=∠BCD,则△BDC∽△ECB,从而证得结论.
(II)由(I)可得到∠BCE=∠BDC,而∠EBC=∠BCD,则△BDC∽△ECB,从而证得结论.
解答:解(I)∵ABCD是圆的内接四边形,
∴∠CAE=∠BDC,
又∵EC与圆相切于点C,
∴∠ACE=∠ABC.
∵AB∥CD,所以∠DCB=∠ABC,
∴∠ACE=∠DCB,
故∠DBC=∠AEC----------(5分)
(II)∵∠BCE=∠BCA+∠ACE=∠BCA+∠ABC=∠CAE,
∴∠BCE=∠BDC.
又∵∠EBC=∠BCD,
∴△BDC∽△ECB,
即BC2=BE•CD

∴∠CAE=∠BDC,
又∵EC与圆相切于点C,
∴∠ACE=∠ABC.
∵AB∥CD,所以∠DCB=∠ABC,
∴∠ACE=∠DCB,
故∠DBC=∠AEC----------(5分)
(II)∵∠BCE=∠BCA+∠ACE=∠BCA+∠ABC=∠CAE,
∴∠BCE=∠BDC.
又∵∠EBC=∠BCD,
∴△BDC∽△ECB,
即BC2=BE•CD
点评:本题主要考查了圆的内接四边形的性质,以及三角形相似,同时考查了分析问题的能力.

练习册系列答案
相关题目
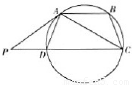
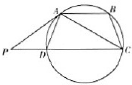 如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明:
如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明: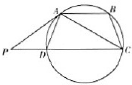 如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明:
如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明: