题目内容
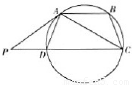
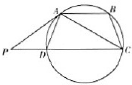 如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明:
如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明:
(1)∠PAD=∠CAB;
(2)AD2=AB•PD.
解:(1)∵AB∥CD,∴∠ACD=∠CAB
∵AP切圆于A点,∠PAD夹弧AD
∴∠PAD=∠ACD,可得∠PAD=∠CAB;
(2)∵ABCD是圆的内接四边形,
∴∠ADP=∠CBA
∵∠PAD=∠CAB,
∴△PAD∽△CAB,可得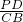 =
=
∵AB、CD是圆的平行弦
∴CB=AD,可得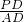 =
= ,得AD2=AB•PD.
,得AD2=AB•PD.
分析:(1)根据平行线的内错角相等,得∠ACD=∠CAB,再由弦切角定理,得∠PAD=∠ACD,可得∠PAD=∠CAB;
(2)根据圆内接四边形的性质,得∠ADP=∠CBA,结合∠PAD=∠CAB得△PAD∽△CAB,从而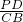 =
= ,最后由圆的平行弦截得弦长相等,得CB=AD,从而得到AD2=AB•PD.
,最后由圆的平行弦截得弦长相等,得CB=AD,从而得到AD2=AB•PD.
点评:本题在圆中证明角相等,并且证明线段的比例中项,着重考查了圆内接四边形的性质、相似三角形和与圆有关的比例线段等知识,属于中档题.
∵AP切圆于A点,∠PAD夹弧AD
∴∠PAD=∠ACD,可得∠PAD=∠CAB;
(2)∵ABCD是圆的内接四边形,
∴∠ADP=∠CBA
∵∠PAD=∠CAB,
∴△PAD∽△CAB,可得
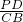 =
=
∵AB、CD是圆的平行弦
∴CB=AD,可得
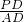 =
= ,得AD2=AB•PD.
,得AD2=AB•PD.分析:(1)根据平行线的内错角相等,得∠ACD=∠CAB,再由弦切角定理,得∠PAD=∠ACD,可得∠PAD=∠CAB;
(2)根据圆内接四边形的性质,得∠ADP=∠CBA,结合∠PAD=∠CAB得△PAD∽△CAB,从而
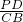 =
= ,最后由圆的平行弦截得弦长相等,得CB=AD,从而得到AD2=AB•PD.
,最后由圆的平行弦截得弦长相等,得CB=AD,从而得到AD2=AB•PD.点评:本题在圆中证明角相等,并且证明线段的比例中项,着重考查了圆内接四边形的性质、相似三角形和与圆有关的比例线段等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
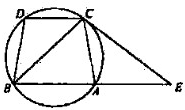 如图,ABCD是圆的内接四边形,AB∥CD,过C点的圆的切线与BA的延长线交于E点,
如图,ABCD是圆的内接四边形,AB∥CD,过C点的圆的切线与BA的延长线交于E点,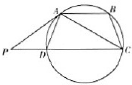 如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明:
如图,ABCD是圆的内接四边形,AB∥CD,过A点的圆的切线与CD的延长线交于P点,证明: