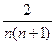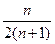题目内容
.(本小题满分12分)
已知数列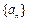 满足:
满足: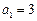 ,
,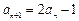 ,
,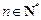 .计算得
.计算得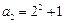 ,
, .
.
(1)猜想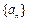 的通项公式
的通项公式 ,并用数学归纳法加以证明;
,并用数学归纳法加以证明;
(2)用反证法证明数列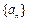 中不存在成等差数列的三项.
中不存在成等差数列的三项.
已知数列
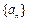 满足:
满足: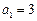 ,
,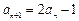 ,
,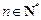 .计算得
.计算得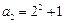 ,
, .
.(1)猜想
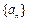 的通项公式
的通项公式 ,并用数学归纳法加以证明;
,并用数学归纳法加以证明;(2)用反证法证明数列
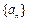 中不存在成等差数列的三项.
中不存在成等差数列的三项.解:(I)猜想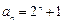 , …………2分
, …………2分
证明如下:
①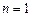 时,
时, ,等式成立;
,等式成立;
②假设当 时等式成立,即
时等式成立,即 ,
,
那么当 时,
时, ,
,
所以当 时等式也成立,
时等式也成立,
由①②可知,等式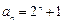 对
对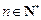 成立; …………6分
成立; …………6分
(II)假设数列 中存在成等差数列的三项
中存在成等差数列的三项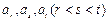 ,则
,则 ,….8分
,….8分
∵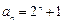 ,∴
,∴ ,即
,即
∴ ,
,
因此,数列 中不存在成等差数列的三项. …………12分
中不存在成等差数列的三项. …………12分
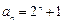 , …………2分
, …………2分证明如下:
①
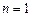 时,
时, ,等式成立;
,等式成立;②假设当
 时等式成立,即
时等式成立,即 ,
,那么当
 时,
时, ,
,所以当
 时等式也成立,
时等式也成立,由①②可知,等式
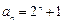 对
对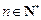 成立; …………6分
成立; …………6分(II)假设数列
 中存在成等差数列的三项
中存在成等差数列的三项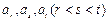 ,则
,则 ,….8分
,….8分∵
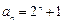 ,∴
,∴ ,即
,即
∴
 ,
,
因此,数列
 中不存在成等差数列的三项. …………12分
中不存在成等差数列的三项. …………12分略

练习册系列答案
相关题目
 (
(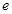 是自然对数的底数)
是自然对数的底数)
 的最小值;
的最小值; 的解集为P, 若
的解集为P, 若
 的取值范围;
的取值范围; ,是否存在等差数列
,是否存在等差数列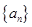 和首项为
和首项为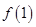 公比大于0的等比数列
公比大于0的等比数列 ,使数列
,使数列 的前n项和等于
的前n项和等于
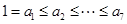 ,其中
,其中 成公比为q的等比数列,
成公比为q的等比数列,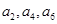 成公差为1的等差数列,则q的最小值是________
成公差为1的等差数列,则q的最小值是________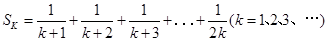 ,则
,则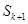 等于( )
等于( )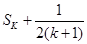
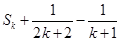
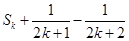

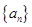 是公差为2的等差数列,且
是公差为2的等差数列,且 成等比数列,则
成等比数列,则 为( )
为( ) 对任意的正整数n,都有
对任意的正整数n,都有 (d为常数),则称
(d为常数),则称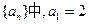 ,“绝对公和”
,“绝对公和”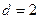 ,则其前2010项和
,则其前2010项和 的最小值为
的最小值为  ,则
,则 等于( )
等于( ) 



 满足
满足 ,且
,且 。
。 ,
,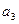 ,
, 的值;
的值; 中,
中,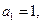 前
前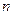 项和为
项和为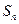 ,且点
,且点 在直线
在直线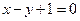 上,则
上,则 =( )
=( )