题目内容
制定投资计划时,不仅要考虑可能获得的赢利,而且要考虑可能出现的亏损。某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大赢利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的赢利最大?
【答案】
投资人分别用4万元、6万元投资甲、乙两个项目,赢利最大为7万元。
【解析】
试题分析:设投资人分别用x万元、y万元投资甲、乙两个项目,由题意知
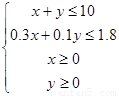 ,目标函数为z=x+0.5y,画出可行域和直线x+0.5y=0并平移得到最优点是直线x+y=10与直线0.3x+0.1y=1.8的交点(4,6)此时z=7(万元)。
,目标函数为z=x+0.5y,画出可行域和直线x+0.5y=0并平移得到最优点是直线x+y=10与直线0.3x+0.1y=1.8的交点(4,6)此时z=7(万元)。
故投资人分别用4万元、6万元投资甲、乙两个项目,赢利最大为7万元。
考点:本题主要考查简单线性规划。
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.

练习册系列答案
相关题目
 万元投资甲项目,
万元投资甲项目, 万元投资乙项目,试写出
万元投资乙项目,试写出