题目内容
[番茄花园1] 在平行四边形ABCD中，O是AC与BD的交点，P、Q、M、N分别是线段OA、OB、OC、OD的中点，在APMC中任取一点记为E，在B、Q、N、D中任取一点记为F，设G为满足向量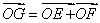
的点，则在上述的点G组成的集合中的点，落在平行四边形ABCD外（不含边界）的概率为 。
[番茄花园1]1.
练习册系列答案
黄冈冠军课课练系列答案
相关题目
黄冈冠军课课练系列答案题目内容
[番茄花园1] 在平行四边形ABCD中，O是AC与BD的交点，P、Q、M、N分别是线段OA、OB、OC、OD的中点，在APMC中任取一点记为E，在B、Q、N、D中任取一点记为F，设G为满足向量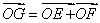的点，则在上述的点G组成的集合中的点，落在平行四边形ABCD外（不含边界）的概率为 。
[番茄花园1]1.
黄冈冠军课课练系列答案
前n项和
满足条件
.
的通项公式；
的前n项和
.
在
中，D为BC边上一点，
,
,
.若
,则BD=_____
在△ABC中，D为边BC上一点，BD=
DC，
ADB=120°，AD=2，若△ADC的面积为
，则