题目内容
【题目】已知点![]() ,平面直角坐标系上的一个动点
,平面直角坐标系上的一个动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)点![]() 是曲线
是曲线![]() 上的任意一点,
上的任意一点,![]() 为圆
为圆![]() 的任意一条直径,求
的任意一条直径,求![]() 的取值范围;
的取值范围;
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)由于动点![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,所以根据椭圆定义可知,
,所以根据椭圆定义可知,![]() 点轨迹是以
点轨迹是以![]() 为焦点,以
为焦点,以![]() 为长轴长的椭圆,因此
为长轴长的椭圆,因此![]() ,
,![]() ,所以
,所以![]() ,所以椭圆方程为
,所以椭圆方程为![]() ,即曲线
,即曲线![]() 方程为
方程为![]() ;(2)根据题意分析,应从问题
;(2)根据题意分析,应从问题![]() 入手,根据平面向量运算可知
入手,根据平面向量运算可知![]() ,
,![]() ,由于
,由于![]() 为圆
为圆![]() 的直径,所以有
的直径,所以有![]() ,因此
,因此![]() ,而
,而![]() ,所以问题转化为求
,所以问题转化为求![]() 的取值范围,设
的取值范围,设![]() ,
,![]() =
=![]() ,由于
,由于![]() ,所以
,所以![]() .
.
试题解析:(1)依据题意,动点![]() 满足
满足![]() .
.
又![]() ,
,
因此,动点![]() 的轨迹是焦点在
的轨迹是焦点在![]() 轴上的椭圆,且
轴上的椭圆,且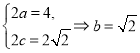 .
.
所以,所求曲线![]() 的轨迹方程是
的轨迹方程是![]() .
.
(2) 设![]() 是曲线
是曲线![]() 上任一点.依据题意,可得
上任一点.依据题意,可得![]() .
.
![]()
![]() 是直径,
是直径,
![]()
![]() .又
.又![]() ,
,
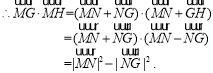
![]()
![]() =
=![]() .
.
由![]() ,可得
,可得![]() ,即
,即![]() .
.
![]() .
.
![]()
![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目