题目内容
设椭圆C: 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o, .
.
求椭圆C的离心率;
如果|AB|= ,求椭圆C的方程.
,求椭圆C的方程.
【答案】
(Ⅰ)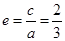 .(Ⅱ)
.(Ⅱ) .
.
【解析】
试题分析:设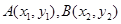 ,由题意知
,由题意知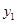 <0,
<0,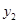 >0.
>0.
(Ⅰ)直线l的方程为 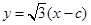 ,其中
,其中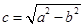 .
.
联立 得
得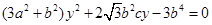
解得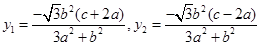
因为 ,所以
,所以 .
.
即 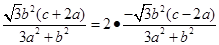
得离心率 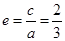 . ……6分
. ……6分
(Ⅱ)因为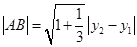 ,所以
,所以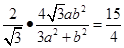 .
.
由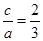 得
得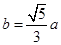 .所以
.所以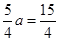 ,得a=3,
,得a=3,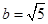 .
.
椭圆C的方程为 . ……12
. ……12
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,共线向量。
点评:中档题,涉及椭圆的题目,在近些年高考题中是屡见不鲜,往往涉及求椭圆标准方程,研究直线与椭圆的位置关系。求椭圆的标准方程,主要考虑定义、a,b,c,e的关系,涉及直线于椭圆位置关系问题,往往应用韦达定理。

练习册系列答案
相关题目

 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,过点
,过点 直线交椭圆
直线交椭圆 于另外一点
于另外一点 ,交
,交 轴正半轴于点
轴正半轴于点 ,
,
 三点的圆恰好与直线
三点的圆恰好与直线
 相切,求椭圆C的方程. (6分)
相切,求椭圆C的方程. (6分)
 的左焦点为F,上顶点为A,过点A作垂直于AF
的左焦点为F,上顶点为A,过点A作垂直于AF ,则椭圆C的离心率为
,则椭圆C的离心率为 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o, .
. ,求椭圆C的方程.
,求椭圆C的方程.