题目内容
 (2013•济南二模)已知四边形ABCD是菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,G、H分别是CE、CF的中点.
(2013•济南二模)已知四边形ABCD是菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,G、H分别是CE、CF的中点.(1)求证:平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°,求直线CF与平面BDGH所成的角的正弦值.
分析:(1)平面AEF内两条相交直线EF与OG分别平行平面BDGH内的两条相交直线GH与OG,利用平面与平面平行的判定定理证明即可.
(2)取EF的中点N,建立空间直角坐标系,设AB=2,BF=t,求出B、C、F、H坐标,求出平面BDGH的一个法向量,平面ABCD的法向量,利用向量的数量积,结合二面角的大小,求出t,然后求出直线CF与平面BDGH所成的角的正弦值.
(2)取EF的中点N,建立空间直角坐标系,设AB=2,BF=t,求出B、C、F、H坐标,求出平面BDGH的一个法向量,平面ABCD的法向量,利用向量的数量积,结合二面角的大小,求出t,然后求出直线CF与平面BDGH所成的角的正弦值.
解答: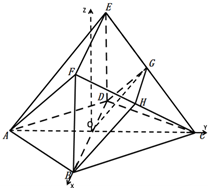 解:(1)G、H分别是CE、CF的中点
解:(1)G、H分别是CE、CF的中点
所以EF∥GH--------①--------(1分)
连接AC与BD交与O,因为四边形ABCD是菱形,所以O是AC的中点
连OG,OG是三角形ACE的中位线OG∥AE---------②-------3 分
由①②知,平面AEF∥平面BDGH--------------(4分)
(2)BF⊥BD,平面BDEF⊥平面ABCD,所以BF⊥平面ABCD---------(5分)
取EF的中点N,ON∥BF∴ON⊥平面ABCD,
建系{
,
,
}
设AB=2,BF=t,
则B(1,0,0),C(0,
,0),F(1,0,t),H(
,
,
)---------------(6分)
=(1,0,0),
=(
,
,
)
设平面BDGH的法向量为
=(x,y,z)
,
所以
=(0,-t,
)
平面ABCD的法向量
=(0,0,1)---------------------------(9分)
|cos<
,
>|=
=
,所以t2=9,t=3---------------(10分)
所以
=(1,-
,3),
设直线CF与平面BDGH所成的角为θ,
sinθ=|cos?
,
>|=
=
-----------------(12分)
 解:(1)G、H分别是CE、CF的中点
解:(1)G、H分别是CE、CF的中点所以EF∥GH--------①--------(1分)
连接AC与BD交与O,因为四边形ABCD是菱形,所以O是AC的中点
连OG,OG是三角形ACE的中位线OG∥AE---------②-------3 分
由①②知,平面AEF∥平面BDGH--------------(4分)
(2)BF⊥BD,平面BDEF⊥平面ABCD,所以BF⊥平面ABCD---------(5分)
取EF的中点N,ON∥BF∴ON⊥平面ABCD,
建系{
| OB |
| OC |
| ON |
设AB=2,BF=t,
则B(1,0,0),C(0,
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| t |
| 2 |
| OB |
| OH |
| 1 |
| 2 |
| ||
| 2 |
| t |
| 2 |
设平面BDGH的法向量为
| n1 |
|
所以
| n1 |
| 3 |
平面ABCD的法向量
| n2 |
|cos<
| n1 |
| n2 |
| ||
|
| 1 |
| 2 |
所以
| CF |
| 3 |
设直线CF与平面BDGH所成的角为θ,
sinθ=|cos?
| CF |
| n1 |
6
| ||||
|
3
| ||
| 13 |
点评:本题考查空间向量求解二面角以及直线与平面所成角的求法,平面与平面平行的判定定理的应用,考查空间想象能力,逻辑推理能力以及计算能力的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目