题目内容
设a>0,f(x)=
是R上的偶函数，(1)求a的值；(2)证明： f(x)在(0，+∞)上是增函数.
（1）a=1
解析:
依题意，对一切x∈R,有f(x)=f(－x),即
+aex.整理，
得(a－
) (ex－
)=0.因此，有a－=0,即a2=1,又a>0,∴a=1
(2)设0＜x1＜x2,则f(x1)－f(x2)=
由x1>0,x2>0,x2>x1,∴
>0,1－e
＜0,
∴f(x1)－f(x2)＜0,即f(x1)＜f(x2)
∴f(x)在(0,+∞)上是增函数
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
是R上的偶函数，(1)求a的值；(2)证明: f(x)在(0，+∞)上是增函数. 
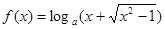(x≥1)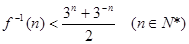
，求a的取值范围。