题目内容
已知函数f(x)=
（1）若函数y=f（x）的图象与直线kx-y-k+1=0有两个交点，求实数k的取值范围．
（2）试求函数g（x）=xf（x）的值域．
|
（1）若函数y=f（x）的图象与直线kx-y-k+1=0有两个交点，求实数k的取值范围．
（2）试求函数g（x）=xf（x）的值域．
分析：（1）作出图象，利用数形结合法即可求解，注意直线kx-y-k+1=0恒过定点（1，1）．
（2）求出函数g（x）的表达式，求分段函数的值域，要先求函数在各段的值域，然后求并集即可．
（2）求出函数g（x）的表达式，求分段函数的值域，要先求函数在各段的值域，然后求并集即可．
解答：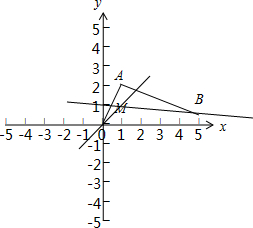
解：（1）直线kx-y-k+1=0，可化为y-1=k（x-1），所以该直线过定点M（1，1）．
如下图所示：B（5，
），kMB=
=-
，kMO=1，
由图象可知kMB≤k≤kMO，即-
≤k≤1．
故实数k的取值范围为[-
，1]．
（2）g（x）=xf（x）=
①当0≤x≤1时，0≤g（x）≤2；
②当1＜x≤5时，g（x）=-
(x-3)2+
，此时2≤g（x）≤
．
综上，函数g（x）的值域为[0，
]．
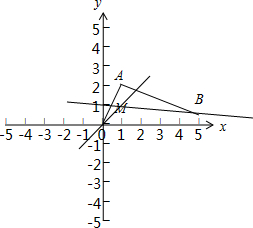解：（1）直线kx-y-k+1=0，可化为y-1=k（x-1），所以该直线过定点M（1，1）．如下图所示：B（5，
| 2 |
| 5 |
1-
| ||
| 1-5 |
| 3 |
| 20 |
由图象可知kMB≤k≤kMO，即-
| 3 |
| 20 |
故实数k的取值范围为[-
| 3 |
| 20 |
（2）g（x）=xf（x）=
|
①当0≤x≤1时，0≤g（x）≤2；
②当1＜x≤5时，g（x）=-
| 2 |
| 5 |
| 18 |
| 5 |
| 18 |
| 5 |
综上，函数g（x）的值域为[0，
| 18 |
| 5 |
点评：本题主要考查了二次函数的图象和性质以及分段函数值域的求解．要深刻理解“三个二次”之间的关系，注意数形结合思想在解题中的应用．
练习册系列答案
相关题目