题目内容
已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c.向量 ,
, 满足
满足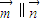 .
.(1)求sinA+sinB的取值范围;
(2)若A
 ,且实数x满足abx=a-b,试确定x的取值范围.
,且实数x满足abx=a-b,试确定x的取值范围.
【答案】分析:(1)由向量平行的坐标表示及正弦定理可得4sinAsinB=4cosAcosB,然后利用两角和的余弦公式可求A+B,然后利用辅助角公式及正弦函数的性质可求
(2)由题意可得,x= =
=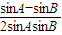 =
=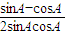 ,利用换元法设t=sinA-cosA,利用同角平方关系可把2sinAcosA用t表示,结合函数的导数可判断函数的单调性进而可求取值范围
,利用换元法设t=sinA-cosA,利用同角平方关系可把2sinAcosA用t表示,结合函数的导数可判断函数的单调性进而可求取值范围
解答:解:(1)∵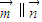
由向量平行的坐标表示可得,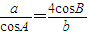 即ab=4cosAcosB
即ab=4cosAcosB
∵△ABC的外接圆半径为1
由正弦定理可得,4sinAsinB=4cosAcosB
∴cosAcosB-sinAsinB=0即cos(A+B)=0
∵0<A+B<π
∴A+B=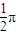 故△ABC为直角三角形
故△ABC为直角三角形
∴sinA+sinB=sinA+cosA=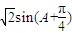
∵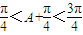
∴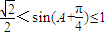
∴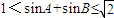
(2)由题意可得,x=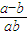 =
=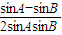 =
=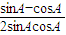
设t=sinA-cosA(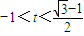 ),则2sinAcosA=1-t2
),则2sinAcosA=1-t2
∴x=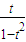
∵=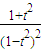 >0
>0
故x=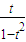 在(-1,
在(-1,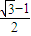 )上单调递增
)上单调递增
∴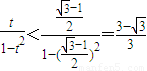
∴x的取值范围是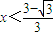
点评:本题综合考查了正弦定理及和差角公式、辅助角公式、同角平方关系及函数的导数与函数的单调性的关系的综合应用
(2)由题意可得,x=
 =
=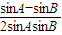 =
=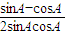 ,利用换元法设t=sinA-cosA,利用同角平方关系可把2sinAcosA用t表示,结合函数的导数可判断函数的单调性进而可求取值范围
,利用换元法设t=sinA-cosA,利用同角平方关系可把2sinAcosA用t表示,结合函数的导数可判断函数的单调性进而可求取值范围解答:解:(1)∵
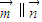
由向量平行的坐标表示可得,
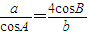 即ab=4cosAcosB
即ab=4cosAcosB∵△ABC的外接圆半径为1
由正弦定理可得,4sinAsinB=4cosAcosB
∴cosAcosB-sinAsinB=0即cos(A+B)=0
∵0<A+B<π
∴A+B=
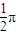 故△ABC为直角三角形
故△ABC为直角三角形∴sinA+sinB=sinA+cosA=
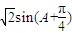
∵
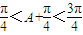
∴
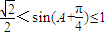
∴
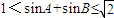
(2)由题意可得,x=
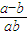 =
=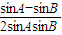 =
=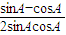
设t=sinA-cosA(
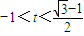 ),则2sinAcosA=1-t2
),则2sinAcosA=1-t2∴x=
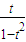
∵=
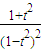 >0
>0故x=
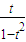 在(-1,
在(-1,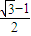 )上单调递增
)上单调递增∴
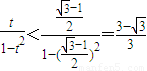
∴x的取值范围是
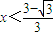
点评:本题综合考查了正弦定理及和差角公式、辅助角公式、同角平方关系及函数的导数与函数的单调性的关系的综合应用

练习册系列答案
相关题目
已知△ABC的外接圆圆心为O,BC>CA>AB.则( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|