题目内容

在三棱锥O—ABC中，三条棱OA、OB、OC两两互相垂直，且OA=OB=OC，M是AB边的中点，则OM与平面ABC所成角的大小是________________（用反三角函数表示）.

解析：如图所示,

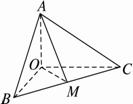
∵OA、OB、OC两两互相垂直，且OA=OB=OC，

∴AB=BC=AC.

    取BC中点M,连结OM和AM,

    则AM⊥BC,OM⊥BC.

∴AM即为OM在ABC面上的射影.

∴∠OMA即为所求.

    又∵△AOM为直角三角形,OA=1,OM=,

∴∠OMA=arctan.

答案:arctan

练习册系列答案
相关题目
如图，在直角三角形ABC中，AD是斜边BC上的高，有很多大家熟悉的性质，例如“AB⊥AC”，勾股定理“|AB|2+|AC|2=|BC|2”和“
1
|AD|2
=
1
|AB|2
+
1
|AC|2
”等，由此联想，在三棱锥O-ABC中，若三条侧棱OA，OB，OC两两互相垂直，可以推出哪些结论？至少写出两个结论．
精英家教网
在Rt△OAB中，∠O=90°，则 cos2A+cos2B=1．根据类比推理的方法，在三棱锥O-ABC中，OA⊥OB，OB⊥OC，OC⊥OA，α、β、γ 分别是三个侧面与底面所成的二面角，则
cos2α+cos2β+cos2γ=1
cos2α+cos2β+cos2γ=1
．
在三棱锥O-ABC中，OA、OB、OC两两垂直，OC=1，OA=x，OB=y，x+y=4，当三棱锥O-ABC的体积最大时，异面直线AB与OC的距离等于
2
2
．
在三棱锥O-ABC中，M，N分别是OA，BC的中点，点G是MN的中点，则
OG
可用基底{
OA
，
OB，
OC
}表示成：
OG
=
1
4
(
OA
+
OB
+
OC
)
1
4
(
OA
+
OB
+
OC
)
．
（2012•安徽模拟）给出下列命题，其中正确的命题是
①③④
①③④
（写出所有正确命题的编号）．
①非零向量
a
、
b
满足|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
+
b
的夹角为30°；
②已知非零向量
a
、
b
，则“
a
•
b
＞0”是“
a
、
b
的夹角为锐角”的充要条件；
③命题“在三棱锥O-ABC中，已知
OP
=x
OA
+y
OB
-2
OC
，若点P在△ABC所在的平面内，则x+y=3”的否命题为真命题；
④若(
AB
+
AC
)•(
AB
-
AC
)=0，则△ABC为等腰三角形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网