题目内容
已知函数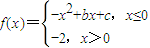 ,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .
,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .
【答案】分析:本题考查的是分段函数以及零点个数问题.在解答时可以先根据条件确定函数f(x)的解析式,然后明确函数g(x)的解析式,进而分析零点个数获得答案
解答:解:由题意可知: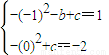
∴b=-4,c=-2,∴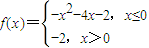 ,
,
∴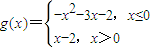 ,
,
当x≤0时,由-x2-3x-2=0,知x=-1或-2;
当x>0时,由x-2=0,知x=2.∴函数g(x)的零点个数为3个.
故答案为:3.
点评:本题考查的是分段函数与零点定理的综合类问题.在解答过程中充分展现了求解析式的知识、解方程的知识以及零点的知识.其中由方程解参数的思想、方程的思想、转化的思想在题目当中得到了灵活应用.值得总结体会.
解答:解:由题意可知:
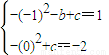
∴b=-4,c=-2,∴
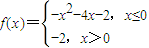 ,
,∴
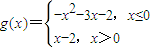 ,
,当x≤0时,由-x2-3x-2=0,知x=-1或-2;
当x>0时,由x-2=0,知x=2.∴函数g(x)的零点个数为3个.
故答案为:3.
点评:本题考查的是分段函数与零点定理的综合类问题.在解答过程中充分展现了求解析式的知识、解方程的知识以及零点的知识.其中由方程解参数的思想、方程的思想、转化的思想在题目当中得到了灵活应用.值得总结体会.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
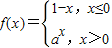 ,若f(1)=f(-1),则实数a的值等于( )
,若f(1)=f(-1),则实数a的值等于( )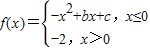 ,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .
,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .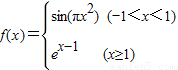 ,若f(1)+f(a)=2,则a的所有可能值为( )
,若f(1)+f(a)=2,则a的所有可能值为( )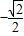
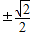
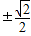
 ,若f(1)=f(-1),则实数a的值等于( )
,若f(1)=f(-1),则实数a的值等于( )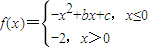 ,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .
,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .