题目内容
有一正三棱锥和一个正四棱锥，它们的所有棱长都相等，把正三棱锥和正四棱锥的一个全等的面重合．①说明组合体是什么样的几何体？
②证明你的结论．
分析：先画出几何体来，由正三棱锥和正四棱锥，它们的所有棱长都相等推知各个面都是正三角形，再由内错角相等可分别证得侧棱平行，由面与面平行的判断定理可证得两个面平面，由斜三棱柱的结构特征得到结论．
解答：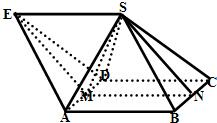
解：（1）如图所示，是斜三棱柱．
（2）正三棱锥为S-AED，正四棱锥为S-ABCD，
重合的面为△ASD，
如图所示，设AD，BC中点分别为M、N，
由AD⊥平面MNS知平面MES重合；
∵SE=AB=MN，EM=SN，
∴MNSE为平行四边行．
∴ES
MN，又AB
MN，
∴ES
AB，
∴四边形ABSE
为平行四边形，CDES为平行四边形．
∴面SBC∥面EAD，
AB∥CD∥SE，且AB不垂
直平面SBC
∴组合体为斜三棱柱．
解：（1）如图所示，是斜三棱柱．（2）正三棱锥为S-AED，正四棱锥为S-ABCD，
重合的面为△ASD，
如图所示，设AD，BC中点分别为M、N，
由AD⊥平面MNS知平面MES重合；
∵SE=AB=MN，EM=SN，
∴MNSE为平行四边行．
∴ES
| ||
. |
| ||
. |
∴ES
| ||
. |
∴四边形ABSE
为平行四边形，CDES为平行四边形．
∴面SBC∥面EAD，
AB∥CD∥SE，且AB不垂
直平面SBC
∴组合体为斜三棱柱．
点评：本题主要考查空间几何体的结构特征及其内在联系．
练习册系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
,
是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和，并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°?
若存在,请具体构造出这样的一个平行六面体,并给出证明；若不存在,请说明理由.