题目内容
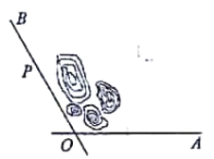
【题目】如图,一岛礁旁有两条航道![]() 与
与![]() ,
,![]() .一日,我方船只甲在
.一日,我方船只甲在![]() 航道上巡逻,在与
航道上巡逻,在与![]() 相距50公里的点
相距50公里的点![]() 处,发现不明身份的船乙刚驶过点
处,发现不明身份的船乙刚驶过点![]() ,并沿
,并沿![]() 方向以40公里/小时的速度运动,船甲立即沿
方向以40公里/小时的速度运动,船甲立即沿![]() 方向以
方向以![]() 公里/小时(
公里/小时(![]() )的速度追击,且甲到达点
)的速度追击,且甲到达点![]() 即停止前行(乙可继续前进).设甲出发时,经过
即停止前行(乙可继续前进).设甲出发时,经过![]() 小时甲,乙之间的距离为
小时甲,乙之间的距离为![]() 公里,当
公里,当![]() 最小时,可以达到最佳的驱离距离.
最小时,可以达到最佳的驱离距离.
(1)试求![]() 的解析式,并写出定义域;
的解析式,并写出定义域;
(2)求最多经过多长时间,我船可以达到最佳的驱离距离?
【答案】(1)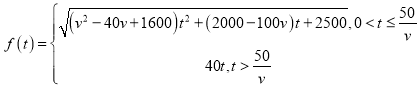 ;(2)
;(2)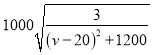 .
.
【解析】
(1)根据题意,结合余弦定理,即可容易求得解析式和定义域;
(2)根据(1)中所求,求得![]() 的最小值即可.
的最小值即可.
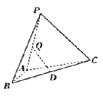
(1)设经过![]() 小时,甲到达
小时,甲到达![]() 点,乙到达
点,乙到达![]() 点,如下图所示:
点,如下图所示:

在![]() 中,
中,![]() ,
,
由余弦定理可得![]()
![]() ;
;
当![]() ,甲到达
,甲到达![]() 点,乙继续前进,故
点,乙继续前进,故![]() ;
;
综上所述: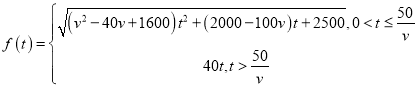 ,
,
(2)当![]() ,
,
![]()
其对称轴为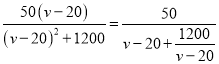 ,因为
,因为![]() ,
,
故可得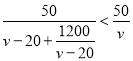 ,
,
则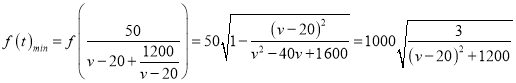 ,
,
当![]() 时,该函数是单调增函数,故
时,该函数是单调增函数,故![]() .
.
综上所述,![]() 的最小值为
的最小值为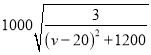 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目