题目内容
(本小题满分14分)
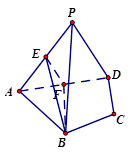
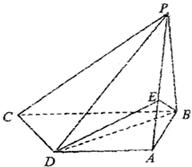
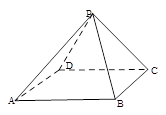
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA,AC、CB、BP的中点.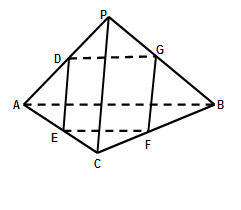
(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,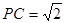 ,求四面体PABC的体积.
,求四面体PABC的体积.
(1)只需证DG//EF; (2)只需证AB⊥面POC;(3)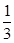 。
。
解析试题分析:(1)依题意DG//AB……1分,
EF∥AB…2分,
所以DG//EF……3分,
DG、EF共面,从而D、E、F、G四点共面……4分。
(2)取AB中点为O,连接PO、CO……5分
因为PA=PB, CA=CB,所以PO⊥AB,CO⊥AB……7分,
因为PO∩CO=D,所以AB⊥面POC……8分
PC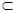 面POC,所以AB⊥PC……9分
面POC,所以AB⊥PC……9分
(3)因为△ABC和PAB是等腰直角三角形,所以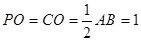 …10分,
…10分,
因为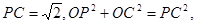 所以OP⊥OC……11分,
所以OP⊥OC……11分,
又PO⊥AB,且AB∩OC=O,所以PO⊥面ABC……12分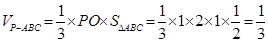 ……14分(公式1分,其他1分)
……14分(公式1分,其他1分)
考点:平面的基本性质与推理;线面垂直的性质定理;棱锥的体积公式。
点评:第三问,把三棱锥P-ABC体积的求法转化为求棱锥A-POB和棱锥B-POC的体积之和是解决问题的关键。

练习册系列答案
相关题目
 所在平面与正
所在平面与正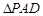 所在平面互相垂直,
所在平面互相垂直,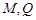 分别为
分别为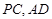 的中点.
的中点.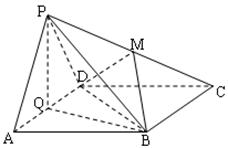
 -
- 的体积;
的体积; 平面
平面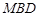 ;
;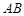 上是否存在一点
上是否存在一点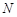 ,使得平面
,使得平面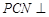 平面
平面 ?若存在,试指出点
?若存在,试指出点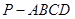 中,侧棱
中,侧棱 的长为
的长为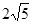 ,
,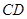 所成的角的大小等于
所成的角的大小等于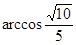 .
.
 的表面上,求此球
的表面上,求此球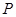 是四边形
是四边形 所在平面外一点,四边形
所在平面外一点,四边形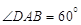 的菱形,侧面
的菱形,侧面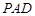
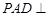 平面
平面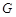 为
为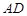 边的中点,求证:
边的中点,求证: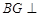 平面
平面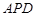 .
.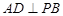 .
. 中,棱长
中,棱长 ,
, 、
、 分别为
分别为 、
、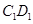 的中点,
的中点,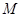 、
、 是
是 、
、 的中点,
的中点,
 //平面
//平面 ;
; 到平面
到平面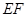 ⊥平面
⊥平面 ,
,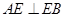 ,
,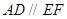 ,
,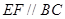 ,
,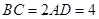 ,
,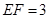 ,
,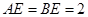 ,
,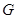 是
是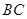 的中点.
的中点.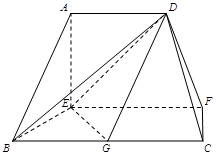
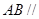 平面
平面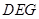 ;
;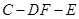 的余弦值.
的余弦值.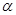 //平面
//平面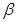 ,AB、CD是夹在
,AB、CD是夹在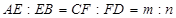 ,求证:
,求证: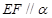 .
.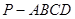 中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点