题目内容
箱子里装有10个大小相同的编号为1、2、3的小球,其中1号小球有2个,2号小球有m,3号小球有n个,且m<n.从箱子里一次摸出两个球号码是2号和3号各一个的概率是
(1)求m,n的值;
(2)从箱子里一次任意摸出两个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列和数学期望.
【答案】分析:(1)根据从箱子里一次摸出两个球号码是2号和3号各一个的概率是 ,利用古典概型的概率公式可建立方程,借助于共有10个球,可得另一方程,从而可求m,n的值;
,利用古典概型的概率公式可建立方程,借助于共有10个球,可得另一方程,从而可求m,n的值;
(2)从箱子里一次任意摸出两个球,设得到小球的编号数之和为ξ,则ξ的可能取值为2,3,4,5,6,利用古典概型的概率公式可求随机变量ξ的分布列和数学期望
解答:解:(1)由已知有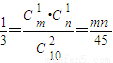 ,∴mn=15,(2分)
,∴mn=15,(2分)
又m+n=8,m<n,∴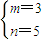 (4分)
(4分)
(2)ξ的可能取值为2,3,4,5,6(5分)
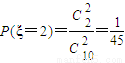
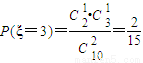
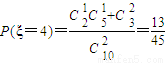
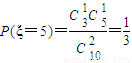
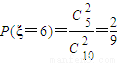 (10分)
(10分)
ξ的分布列为
ξ的数学期望为: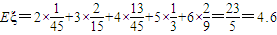 (12分)
(12分)
点评:本题以摸球为素材,考查离散型随机变量的分布列及数学期望,解题的关键是确定随机变量的取值,理解其意义,从而合理运用公式求解.
 ,利用古典概型的概率公式可建立方程,借助于共有10个球,可得另一方程,从而可求m,n的值;
,利用古典概型的概率公式可建立方程,借助于共有10个球,可得另一方程,从而可求m,n的值;(2)从箱子里一次任意摸出两个球,设得到小球的编号数之和为ξ,则ξ的可能取值为2,3,4,5,6,利用古典概型的概率公式可求随机变量ξ的分布列和数学期望
解答:解:(1)由已知有
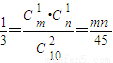 ,∴mn=15,(2分)
,∴mn=15,(2分)又m+n=8,m<n,∴
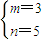 (4分)
(4分)(2)ξ的可能取值为2,3,4,5,6(5分)
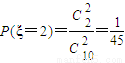
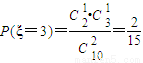
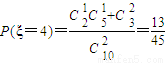
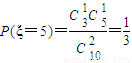
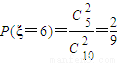 (10分)
(10分)ξ的分布列为
| ξ | 2 | 3 | 4 | 5 | 6 |
| P | 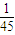 | 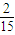 | 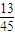 |  |  |
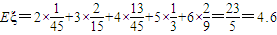 (12分)
(12分)点评:本题以摸球为素材,考查离散型随机变量的分布列及数学期望,解题的关键是确定随机变量的取值,理解其意义,从而合理运用公式求解.

练习册系列答案
相关题目

