题目内容
13.已知sin($\frac{π}{6}-α$)=$\frac{1}{3}$,则sin($\frac{π}{6}+2α$)=( )| A. | -$\frac{2\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{2}}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
分析 根据三角函数的诱导公式,结合余弦函数的倍角公式进行化简即可.
解答 解:sin($\frac{π}{6}+2α$)=cos[$\frac{π}{2}$-($\frac{π}{6}+2α$)]=cos($\frac{π}{3}-2α$)=cos2($\frac{π}{6}-α$)=1-2sin2($\frac{π}{6}-α$)
=1-2×($\frac{1}{3}$)2=1-$\frac{2}{9}$=$\frac{7}{9}$,
故选:D.
点评 本题主要考查三角函数值的计算,根据三角函数的诱导公式以及余弦函数的倍角公式是解决本题的关键.

练习册系列答案
相关题目
1.已知i为虚数单位,则复数$\frac{1-3i}{1+i}$=( )
| A. | 2+i | B. | 2-i | C. | -1-2i | D. | -1+2i |
18.两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
| A. | akm | B. | $\sqrt{2}$akm | C. | 2akm | D. | $\sqrt{3}$akm |
3.已知实数x、y满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≥0}\\{x≥0}\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | 5 | D. | 9 |
20.已知集合A={0,b},B={x∈Z|x2-3x<0},若A∩B≠∅,则b等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或2 |
 ,
,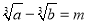 ,
,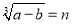 ,则有( )
,则有( )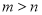 B.
B.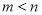
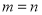 D.
D.