题目内容
过双曲线2x2-y2=1上一点A(1,1)作两条动弦AB,AC,且直线AB,AC的斜率的乘积为3.
(1)问直线BC是否可与坐标轴垂直?若可与坐标轴垂直,求直线BC的方程,若不与坐标轴垂直,试说明理由.
(2)证明直线BC过定点.
(1)解:令B(x1,y1),C(x2,y2).
当BC与x轴垂直时,有x1=x2,y1=-y2,
故:3=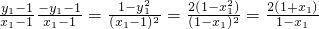
∴x1= ,与|x1|≥
,与|x1|≥ 矛盾,因此BC不与x轴垂直..(3分)
矛盾,因此BC不与x轴垂直..(3分)
当BC与y轴垂直时,有x1=-x2,y1=y2,
故:3=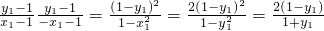
∴y1=- ,因此BC可与y轴垂直,此时BC的方程为y=-
,因此BC可与y轴垂直,此时BC的方程为y=- .(5分)
.(5分)
(2)证明:当BC不与坐标轴垂直时,kAB•kAC=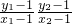 =3,
=3,
故3(x1-1)(x2-1)=(y1-1)(y2-1).…①…(6分)
令BC:y=kx+b,代入双曲线方程有:2x2-(kx+b)2=1?(2-k2)x2-2kbx-b2-1=0.…②
x1,x2是方程②的两个实根.令f(x)=(2-k2)x2-2kbx-b2-1,
则(x1-1)(x2-1)=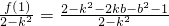 .③…..(8分)
.③…..(8分)
直线方程又可写成:x=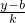 ,代入2x2-y2=1,有:2(y-b)2-k2y2=k2,整理得:(2-k2)y2-4by+2b2-k2=0.…④
,代入2x2-y2=1,有:2(y-b)2-k2y2=k2,整理得:(2-k2)y2-4by+2b2-k2=0.…④
y1,y2是方程④的两个实根.
令g(y)=(2-k2)y2-4by+2b2-k2.
(y1-1)(y2-1)=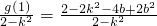 .…⑤…(10分)
.…⑤…(10分)
③,⑤两式代入①式,有: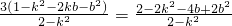 ,
,
故3[1-(k+b)2]=2[(b-1)2-k2],
从而:3(1-k-b)(1+k+b)=2(b-1-k)(b-1+k).…⑥
因为点A(1,1)不在直线y=kx+b上,故k+b≠1.
利用⑥,可知:3 (1+k+b)+2(b-1-k)=0,
即k+5b+1=0,所以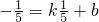 .
.
因此直线BC过定点M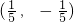 ,直线y=-
,直线y=- 也过定点M.
也过定点M.
综上所述,直线BC恒过定点M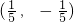 .…(14分)
.…(14分)
分析:(1)分类讨论,利用直线AB,AC的斜率的乘积为3,即可求得结论;
(2)令BC:y=kx+b,代入双曲线方程,得出k+5b+1=0,所以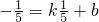 ,因此直线BC过定点M
,因此直线BC过定点M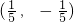 ,直线y=-
,直线y=- 也过定点,从而可得结论.
也过定点,从而可得结论.
点评:本题考查直线与双曲线的位置关系,考查直线恒过定点,考查学生的计算能力,难度较大.
当BC与x轴垂直时,有x1=x2,y1=-y2,
故:3=
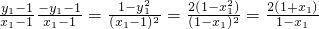
∴x1=
 ,与|x1|≥
,与|x1|≥ 矛盾,因此BC不与x轴垂直..(3分)
矛盾,因此BC不与x轴垂直..(3分)当BC与y轴垂直时,有x1=-x2,y1=y2,
故:3=
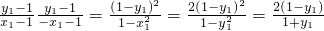
∴y1=-
 ,因此BC可与y轴垂直,此时BC的方程为y=-
,因此BC可与y轴垂直,此时BC的方程为y=- .(5分)
.(5分)(2)证明:当BC不与坐标轴垂直时,kAB•kAC=
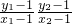 =3,
=3,故3(x1-1)(x2-1)=(y1-1)(y2-1).…①…(6分)
令BC:y=kx+b,代入双曲线方程有:2x2-(kx+b)2=1?(2-k2)x2-2kbx-b2-1=0.…②
x1,x2是方程②的两个实根.令f(x)=(2-k2)x2-2kbx-b2-1,
则(x1-1)(x2-1)=
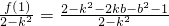 .③…..(8分)
.③…..(8分)直线方程又可写成:x=
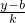 ,代入2x2-y2=1,有:2(y-b)2-k2y2=k2,整理得:(2-k2)y2-4by+2b2-k2=0.…④
,代入2x2-y2=1,有:2(y-b)2-k2y2=k2,整理得:(2-k2)y2-4by+2b2-k2=0.…④y1,y2是方程④的两个实根.
令g(y)=(2-k2)y2-4by+2b2-k2.
(y1-1)(y2-1)=
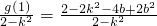 .…⑤…(10分)
.…⑤…(10分) ③,⑤两式代入①式,有:
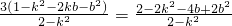 ,
,故3[1-(k+b)2]=2[(b-1)2-k2],
从而:3(1-k-b)(1+k+b)=2(b-1-k)(b-1+k).…⑥
因为点A(1,1)不在直线y=kx+b上,故k+b≠1.
利用⑥,可知:3 (1+k+b)+2(b-1-k)=0,
即k+5b+1=0,所以
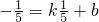 .
. 因此直线BC过定点M
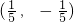 ,直线y=-
,直线y=- 也过定点M.
也过定点M.综上所述,直线BC恒过定点M
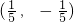 .…(14分)
.…(14分)分析:(1)分类讨论,利用直线AB,AC的斜率的乘积为3,即可求得结论;
(2)令BC:y=kx+b,代入双曲线方程,得出k+5b+1=0,所以
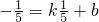 ,因此直线BC过定点M
,因此直线BC过定点M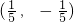 ,直线y=-
,直线y=- 也过定点,从而可得结论.
也过定点,从而可得结论.点评:本题考查直线与双曲线的位置关系,考查直线恒过定点,考查学生的计算能力,难度较大.

练习册系列答案
相关题目