题目内容
构造一个三角函数f(x),使它的最小正周期为4,且满足f(2002)=1,则f(x)的解析式为 .
【答案】分析:根据构造的新函数的周期做出ω的值,根据函数的图象过一个定点,确定函数的初相,注意初相是最难确定的部分.
解答:解:∵构造一个三角函数f(x),使它的最小正周期为4,
∴T=4,
∴ω=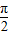 ,
,
∴f(x)=sin(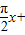 φ)
φ)
∵函数的图象过(2002,1)
∴1=sin(1001π+φ)=sin(π+φ)
∴φ=-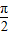
∴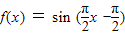
故答案为: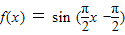 答案不唯一
答案不唯一
点评:本题是基础题,考查三角函数的确定,实际上是一个根据函数的图象确定函数的解析式的题目,考查发现问题解决问题的能力.
解答:解:∵构造一个三角函数f(x),使它的最小正周期为4,
∴T=4,
∴ω=
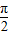 ,
,∴f(x)=sin(
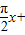 φ)
φ)∵函数的图象过(2002,1)
∴1=sin(1001π+φ)=sin(π+φ)
∴φ=-
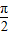
∴
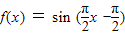
故答案为:
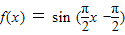 答案不唯一
答案不唯一点评:本题是基础题,考查三角函数的确定,实际上是一个根据函数的图象确定函数的解析式的题目,考查发现问题解决问题的能力.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)