题目内容
已知f(x)＝x3＋ax2＋bx＋a2在x＝1处有极值为10，则a＋b＝________.
－7
【解析】f′(x)＝3x2＋2ax＋b，当x＝1时，函数取得极值10，得
解得
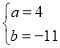或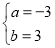
当a＝－3，b＝3时，f′(x)＝3x2－6x＋3＝3(x－1)2在x＝1两侧的符号相同，所以a＝－3，b＝3不符合题意舍去．而a＝4，b＝－11满足f′(x)在x＝1两侧异号，故a＋b＝－7.
练习册系列答案
备战中考寒假系列答案
相关题目
备战中考寒假系列答案题目内容
已知f(x)＝x3＋ax2＋bx＋a2在x＝1处有极值为10，则a＋b＝________.
－7
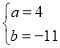【解析】f′(x)＝3x2＋2ax＋b，当x＝1时，函数取得极值10，得解得或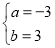当a＝－3，b＝3时，f′(x)＝3x2－6x＋3＝3(x－1)2在x＝1两侧的符号相同，所以a＝－3，b＝3不符合题意舍去．而a＝4，b＝－11满足f′(x)在x＝1两侧异号，故a＋b＝－7.
备战中考寒假系列答案
