题目内容
已知直线L与抛物线C:x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B(2,0)(1)求点A的横坐标.
(2)设动点M满足
| AB |
| BM |
| 2 |
| AM |
分析: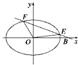 (1)由x2=4y得y=
(1)由x2=4y得y=
x2,用导数法求得直线l的斜率,再求得其方程,令y=0得点A坐标;
(2)设M(x,y由
•
+
|
|=0=0得得
+y2=1.知轨迹K是椭圆,设E(x1,y1),F(x2,y2),
=λ•
,x2<x1,0<λ<1
由两个三角形同底,则
=λ•
,即为两个三角形面积之比,只要求得λ即可.
 (1)由x2=4y得y=
(1)由x2=4y得y=| 1 |
| 4 |
(2)设M(x,y由
| AB |
| BM |
| 2 |
| AM |
| x2 |
| 2 |
| BE |
| BF |
由两个三角形同底,则
| BE |
| BF |
解答: 解:(1)由x2=4y得y=
解:(1)由x2=4y得y=
x2,y′=
x.
∴直线l的斜率为y′|x=2=1.
故l的方程为y=x-1,
∴点A坐标为(1,0).(4分)
(2)设M(x,y),则
=(1,0),
=(x-2,y),
=(x-1,y),
由
•
+
|
|=0=0得(x-2)+y•0+
•
=0,
整理,得
+y2=1.轨迹K是椭圆.(9分)
设E(x1,y1),F(x2,y2),
=λ•
,x2<x1,0<λ<1
从而得
?
因为E、F都在椭圆上,所以满足椭圆方程:
&x22+2•y22=2
消去y2,并整理得
=
-x2①(11分)
由题意,设过点B的直线方程:x=ty+2,
当直线与椭圆相切时,
?(t2+2)y2+4ty+2=0?△y=0
即(4t)2-4•(t2+2)•2=0?t2=2,取t=-
,?y=
?x=1得切点(1,
)
所以知x2∈(-
,1)?
-x2∈(
,
+
)
联系①式知,
∈(
,
)?λ∈(3-2
,1)
即△OBE与△OBF面积之比的取值范围是(3-2
,1).(15分)
 解:(1)由x2=4y得y=
解:(1)由x2=4y得y=| 1 |
| 4 |
| 1 |
| 2 |
∴直线l的斜率为y′|x=2=1.
故l的方程为y=x-1,
∴点A坐标为(1,0).(4分)
(2)设M(x,y),则
| AB |
| BM |
| AM |
由
| AB |
| BM |
| 2 |
| AM |
| 2 |
| (x-1)2+y2 |
整理,得
| x2 |
| 2 |
设E(x1,y1),F(x2,y2),
| BE |
| BF |
从而得
|
|
因为E、F都在椭圆上,所以满足椭圆方程:
|
消去y2,并整理得
| 1 |
| 2λ |
| 3 |
| 2 |
由题意,设过点B的直线方程:x=ty+2,
当直线与椭圆相切时,
|
即(4t)2-4•(t2+2)•2=0?t2=2,取t=-
| 2 |
| ||
| 2 |
| ||
| 2 |
所以知x2∈(-
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
联系①式知,
| 1 |
| 2λ |
| 1 |
| 2 |
3+2
| ||
| 2 |
| 2 |
即△OBE与△OBF面积之比的取值范围是(3-2
| 2 |
点评:本题主要考查导数法求曲线的切线,和用向量法研究直线与曲线的位置关系.

练习册系列答案
相关题目
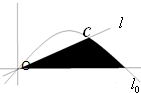 已知直线l与抛物线C,当直线l从l0开始在平面上绕O点按逆时针方向匀速旋转(旋转的角度不超过90°)时,它扫过的面积S是时间t的函数,则函数图象大致是( )
已知直线l与抛物线C,当直线l从l0开始在平面上绕O点按逆时针方向匀速旋转(旋转的角度不超过90°)时,它扫过的面积S是时间t的函数,则函数图象大致是( )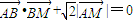 ,点M的轨迹K.若过点B的直线L1(斜率不等于0)与轨迹K交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
,点M的轨迹K.若过点B的直线L1(斜率不等于0)与轨迹K交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.