题目内容
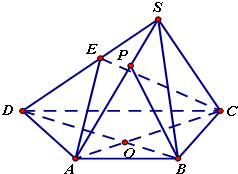 如图,四棱锥S-ABCD中,底面ABCD是等腰梯形,AB∥DC,∠CAB=
如图,四棱锥S-ABCD中,底面ABCD是等腰梯形,AB∥DC,∠CAB=| π |
| 4 |
| 1 |
| 2 |
(Ⅰ)若SB⊥平面ABCD,求证:AC⊥平面SBD;
(Ⅱ)已知点E,P分别在SD,SA上,满足3DE=4ES,AP=2PS.
求证:PB∥面EAC.
分析:(Ⅰ)只要证明AC⊥BD,AC⊥SB即可;
(Ⅱ)连DP交AE于F,只要证明DF:DP=DO:DB=2:3,就能得到OF∥BP,即得证.
(Ⅱ)连DP交AE于F,只要证明DF:DP=DO:DB=2:3,就能得到OF∥BP,即得证.
解答:证明:(Ⅰ)∵四棱锥S-ABCD中,底面ABCD是等腰梯形,AB∥DC,∠CAB=
,AC交BD于O.
∴∠OBA=
,又由∠AOB=π-∠OBA-∠CAB,
所以∠AOB=
,即得AC⊥BD
又∵SB⊥平面ABCD,AC?平面ABCD
∴AC⊥SB,又∵BD∩SB=B
∴AC⊥平面SBD;
(Ⅱ)连接DP交AE于F,连接OF
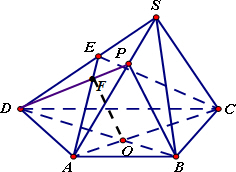
由(Ⅰ)知,AC⊥BD,又由tan∠ACB=tan∠BDA=
,
∴
=
,故
=
又由点E,P分别在SD,SA上,满足3DE=4ES,AP=2PS.
故
=
,所以
=
=
,
∴OF∥BP
又OF?平面ACE,BP?平面ACE
∴BP∥平面ACE.
| π |
| 4 |
∴∠OBA=
| π |
| 4 |
所以∠AOB=
| π |
| 2 |
又∵SB⊥平面ABCD,AC?平面ABCD
∴AC⊥SB,又∵BD∩SB=B
∴AC⊥平面SBD;
(Ⅱ)连接DP交AE于F,连接OF

由(Ⅰ)知,AC⊥BD,又由tan∠ACB=tan∠BDA=
| 1 |
| 2 |
∴
| DO |
| OB |
| 2 |
| 1 |
| DO |
| DB |
| 2 |
| 3 |
又由点E,P分别在SD,SA上,满足3DE=4ES,AP=2PS.
故
| DF |
| DP |
| 2 |
| 3 |
| DF |
| DP |
| 2 |
| 3 |
| DO |
| DB |
∴OF∥BP
又OF?平面ACE,BP?平面ACE
∴BP∥平面ACE.
点评:本题考查直线与平面平行,直线与平面垂直,考查学生转化思想,逻辑思维能力,是中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.