题目内容
如图，矩形ABCD，PA⊥平面ABCD，M、N、R分别是AB、PC、CD的中点．
①求证：直线AR∥平面PMC；②求证：直线MN⊥直线AB．
分析：①由已知中四边形ABCD为矩形，M、R分别是AB、CD的中点．我们易得AR∥CM，结合线面垂直的判定定理，我们易得到直线AR∥平面PMC；
②由已知中PA⊥平面ABCD可得AB⊥PD，又由四边形ABCD为矩形，可得AB⊥平面PAD，即AB⊥PD，又由AD∥MR，PD∥NR，我们易得AB⊥平面MNR，进而得到直线MN⊥直线AB．
②由已知中PA⊥平面ABCD可得AB⊥PD，又由四边形ABCD为矩形，可得AB⊥平面PAD，即AB⊥PD，又由AD∥MR，PD∥NR，我们易得AB⊥平面MNR，进而得到直线MN⊥直线AB．
解答：解：①证明：∵四边形ABCD为矩形，M、R分别是AB、CD的中点．
∴AR∥CM
又∵AR?平面PMC，CM?平面PMC
∴直线AR∥平面PMC；
②连接RN、MR
∵PA⊥平面ABCD?AB⊥PD
AB⊥AD?AB⊥RN
∵R、N分别是CD、PC的中点?RN
PD
∵AB⊥MR?MR∩RN=R（5分）
?AB⊥MN（2分）
∴AR∥CM
又∵AR?平面PMC，CM?平面PMC
∴直线AR∥平面PMC；
②连接RN、MR
∵PA⊥平面ABCD?AB⊥PD
AB⊥AD?AB⊥RN
∵R、N分别是CD、PC的中点?RN
| ∥ |
| 1 |
| 2 |
∵AB⊥MR?MR∩RN=R（5分）
|
点评：本题的知识点是直线与平面平行的判断与直线与平面垂直的性质，其中熟练掌握空间直线与平面关系的判定定理、性质定理、定义是解答本题的关键．
练习册系列答案
相关题目
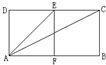如图，矩形ABCD由两个正方形拼成，则∠CAE的正切值为
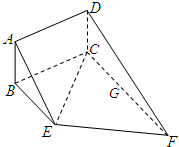如图，矩形ABCD和梯形BEFC所在的平面互相垂直，
（2013•湛江一模）如图，矩形ABCD中，AB=2BC=4，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE