题目内容
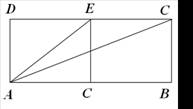
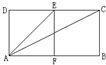如图，矩形ABCD由两个正方形拼成，则∠CAE的正切值为分析：有已知矩形ABCD由两个正方形拼成，设正方形的边长为1，由图可知：∠CAD=∠DAD+CAE，利用两角和的正切公式即可求得．
解答：解：因为矩形ABCD由两个正方形拼成，设正方形的边长为1，
则在Rt△CAD中，tan∠CAD=
=2，∠EAD=
，
所以tan∠CAD=tan(∠CAE+
)?2=
?tan∠CAE=
．
故答案为：
则在Rt△CAD中，tan∠CAD=
| CD |
| AD |
| π |
| 4 |
所以tan∠CAD=tan(∠CAE+
| π |
| 4 |
tan∠CAE+tan
| ||
| 1-tan∠CAE |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：此题考查了识图，还考查了两角和的正切展开式及学生的计算能力．
练习册系列答案
阅读快车系列答案
相关题目
