题目内容
现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为(1)求ξ1、ξ2的概率分布和数学期望Eξ1、Eξ2;
(2)当Eξ1<Eξ2时,求p的取值范围.
(1)解法一:ξ1的概率分布为
ξ1 | 1.2 | 1.18 | 1.17 |
P |
|
|
|
Eξ1=1.2×![]() +1.18×
+1.18×![]() +1.17×
+1.17×![]() =1.18.
=1.18.
由题设得ξ~B(2,p),则ξ的概率分布为
ξ | 0 | 1 | 2 |
P | (1-p)2 | 2p(1-p) | p2 |
故ξ2的概率分布为
ξ2 | 1.3 | 1.25 | 0.2 |
P | (1-p)2 | 2p(1-p) | p2 |
所以ξ2的数学期望为
Eξ2=1.3×(1-p)2+1.25×2p(1-p)+0.2×p2=-p2-0.1p+1.3.
解法二:ξ1的概率分布为
ξ1 | 1.2 | 1.18 | 1.17 |
P |
|
|
|
Eξ1=1.2×![]() +1.18×
+1.18×![]() +1.17×
+1.17×![]() =1.18.
=1.18.
设Ai表示事件”第i次调整,价格下降”(i=1,2),则
P(ξ=0)=P(![]() )P(
)P(![]() )=(1-p)2;
)=(1-p)2;
P(ξ=1)=P(![]() )P(A2)+P(A1)P(
)P(A2)+P(A1)P(![]() )=2p(1-p);
)=2p(1-p);
P(ξ=2)=P(A1)P(A2)=p2.
故ξ2的概率分布为
ξ2 | 1.3 | 1.25 | 0.2 |
P | (1-p)2 | 2p(1-p) | p2 |
所以ξ2的数学期望为
Eξ2=1.3×(1-p)2+1.25×2p(1-p)+0.2×p2=-p2-0.1p+1.3.
(2)解:由Eξ1<Eξ2,得
-p2-0.1p+1.3>1.18![]() (p+0.4)(p-0.3)<0
(p+0.4)(p-0.3)<0![]() -0.4<p<0.3,
-0.4<p<0.3,
因为0<p<1,所以Eξ1<Eξ2时,p的取值范围是0<p<0.3.

练习册系列答案
相关题目
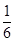 、
、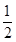 、
、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是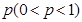 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为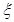 ,对乙项目投资十万元,
,对乙项目投资十万元, 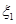 、
、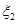 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.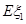 、
、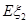 ;
;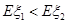 时,求
时,求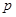 的取值范围.
的取值范围.