题目内容
已知A、B、C三点在曲线y=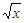 上,其横坐标依次为0,m,4(0<m<4),当△ABC的面积最大时,折线ABC与曲线y=
上,其横坐标依次为0,m,4(0<m<4),当△ABC的面积最大时,折线ABC与曲线y=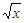 所围成的封闭图形的面积为 .
所围成的封闭图形的面积为 .
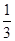
解析试题分析:∵AC边长一定,∴当点B到直线AC距离最大时,△ABC的面积S最大.
∵A(0,0),C(4,2),∴直线AC方程为x-2y=0.
点B(m,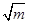 )到直线AC距离d=
)到直线AC距离d=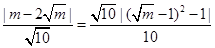 .
.
∵0<m<4,∴0<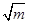 <2,即
<2,即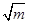 =1,m=1时,d最大,此时△ABC的面积S最大.
=1,m=1时,d最大,此时△ABC的面积S最大.
所以,折线ABC与曲线y=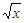 所围成的封闭图形的面积为
所围成的封闭图形的面积为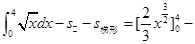
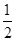 -
- =
=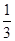 。
。
考点:本题主要考查直线方程,点到直线的距离公式,换元法,二次函数的性质,定积分计算,面积公式。
点评:中档题,本题具有较强的综合性,考查知识点多。通过定积分计算得出曲边梯形的面积,利用间接法求得折线ABC与曲线y=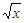 所围成的封闭图形的面积。
所围成的封闭图形的面积。

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
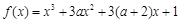 有极大值和极小值,则
有极大值和极小值,则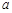 的取值范围是__ .
的取值范围是__ .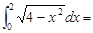 _______________。
_______________。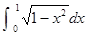 =
=  d
d .
. 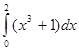 的值为_________.
的值为_________.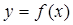 的图象在点P处的切线方程是
的图象在点P处的切线方程是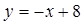 ,则
,则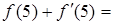

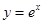 在点
在点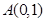 处的切线斜率为 .
处的切线斜率为 .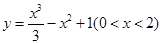 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为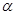 ,则
,则