题目内容
定义 ,已知实数x,y满足|x|≤1,|y|≤1,设z=max{x+y,2x-y},则z的取值范围是 .
,已知实数x,y满足|x|≤1,|y|≤1,设z=max{x+y,2x-y},则z的取值范围是 .
【答案】分析:直线为 AB 将约束条件|x|≤1,|y|≤1,所确定的平面区域分为两部分,如图,令z1=x+y,点(x,y)在四边形ABCD上及其内部,求得- ≤z1≤2;令z2=2x-y,点(x,y)在四边形ABEF上及其内部(除AB边),求得-
≤z1≤2;令z2=2x-y,点(x,y)在四边形ABEF上及其内部(除AB边),求得- ≤z2≤3.
≤z2≤3.
将这两个范围取并集,即为所求.
解答:解:(x+y)-(2x-y)=-x+2y,设方程-x+2y=0 对应的直线为 AB,∴ ,
,
直线为 AB 将约束条件|x|≤1,|y|≤1,所确定的平面区域分为两部分,如图,

令z1=x+y,点(x,y)在四边形ABCD上及其内部,求得- ≤z1≤2;
≤z1≤2;
令z2=2x-y,点(x,y)在四边形ABEF上及其内部(除AB边),求得- ≤z2≤3.
≤z2≤3.
综上可知,z的取值范围为[- ,3].
,3].
故选D.
点评:本题考查不等关系与不等式,简单的线性规划问题的解法,体现了数形结合的数学思想.画出图形,是解题的关键.
 ≤z1≤2;令z2=2x-y,点(x,y)在四边形ABEF上及其内部(除AB边),求得-
≤z1≤2;令z2=2x-y,点(x,y)在四边形ABEF上及其内部(除AB边),求得- ≤z2≤3.
≤z2≤3.将这两个范围取并集,即为所求.
解答:解:(x+y)-(2x-y)=-x+2y,设方程-x+2y=0 对应的直线为 AB,∴
 ,
,直线为 AB 将约束条件|x|≤1,|y|≤1,所确定的平面区域分为两部分,如图,

令z1=x+y,点(x,y)在四边形ABCD上及其内部,求得-
 ≤z1≤2;
≤z1≤2;令z2=2x-y,点(x,y)在四边形ABEF上及其内部(除AB边),求得-
 ≤z2≤3.
≤z2≤3.综上可知,z的取值范围为[-
 ,3].
,3]. 故选D.
点评:本题考查不等关系与不等式,简单的线性规划问题的解法,体现了数形结合的数学思想.画出图形,是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,已知实数x,y满足|x|≤1,|y|≤1,设z=max{x+y,2x-y},则z的取值范围是 .
,已知实数x,y满足|x|≤1,|y|≤1,设z=max{x+y,2x-y},则z的取值范围是 . ,已知实数x,y满足|x|≤1,|y|≤1,设z=max{x+y,2x-y},则z的取值范围是 .
,已知实数x,y满足|x|≤1,|y|≤1,设z=max{x+y,2x-y},则z的取值范围是 .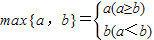 ,已知实数x,y满足|x|≤2,|y|≤2,设z=max{x+y,2y-x},则z的最小值是 .
,已知实数x,y满足|x|≤2,|y|≤2,设z=max{x+y,2y-x},则z的最小值是 .