题目内容
函数f(x)=7sin(
x+
)是( )
| 2 |
| 3 |
| 15π |
| 2 |
分析:根据诱导公式,化简得f(x)=-7cos
x,由三角函数周期公式算出T=3π.再根据余弦函数的奇偶性加以验证,即可得到f(x)为偶函数,得到本题答案.
| 2 |
| 3 |
解答:解:∵f(x)=7sin(
x+
)=7(
x+6π+
)
=7sin(
x+
)=-7sin(x+
)=-7cos
x
∴函数的周期为T=
=3π.
∵f(x)的定义域为R,关于原点对称,
且f(-x)=-7cos(-
x)=-7cos
x=f(x),
∴f(x)为偶函数
故选:A
| 2 |
| 3 |
| 15π |
| 2 |
| 2 |
| 3 |
| 3π |
| 2 |
=7sin(
| 2 |
| 3 |
| 3π |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
∴函数的周期为T=
| 2π | ||
|
∵f(x)的定义域为R,关于原点对称,
且f(-x)=-7cos(-
| 2 |
| 3 |
| 2 |
| 3 |
∴f(x)为偶函数
故选:A
点评:本题给出三角函数表达式,求函数的周期性和奇偶性.着重考查了三角函数的图象与性质的知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
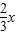 +
+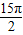 )是( )
)是( )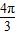 的偶函数
的偶函数