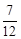题目内容
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为l,2,3,4,5,6点),所得点数分别记为x、y,则x<y的概率为( )
分析:所有的情况共有6×6=36种,其中满足x=y的情况有6种,剩余的30种情况就是x<y和x>y的情况,各占总一半,故满足x<y的情况有15种,由此求得x<y的概率
解答:解:所有的情况共有6×6=36种,其中满足x=y的情况有6种,剩余的30种情况就是x<y和x>y的情况,
各占总一半,故满足x<y的情况有
=15种,故x<y的概率为
=
,
故选C.
各占总一半,故满足x<y的情况有
| 36-6 |
| 2 |
| 15 |
| 36 |
| 5 |
| 12 |
故选C.
点评:本题考查古典概型及其概率计算公式的应用,求得满足x<y的情况有
=15种,是解题的关键,属于基础题.
| 36-6 |
| 2 |

练习册系列答案
相关题目
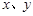 ,则
,则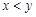 的概率为
的概率为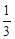 B.
B.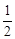 C.
C.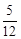 D.
D.