题目内容
如图,在四棱锥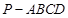 中,底面
中,底面 是菱形,
是菱形,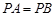 ,且侧面
,且侧面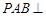 平面
平面 ,点
,点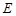 是棱
是棱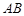 的中点.
的中点.
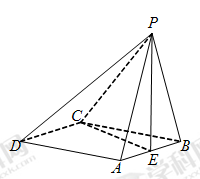
(Ⅰ)求证: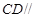 平面
平面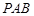 ;
;
(Ⅱ)求证: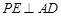 ;
;
(Ⅲ)若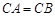 ,求证:平面
,求证:平面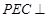 平面
平面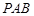 .
.
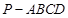 中,底面
中,底面 是菱形,
是菱形,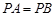 ,且侧面
,且侧面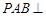 平面
平面 ,点
,点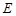 是棱
是棱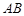 的中点.
的中点.
(Ⅰ)求证:
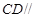 平面
平面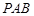 ;
;(Ⅱ)求证:
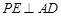 ;
;(Ⅲ)若
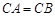 ,求证:平面
,求证:平面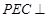 平面
平面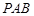 .
.详见解析.
试题分析:(Ⅰ)由底面
 是菱形,可得
是菱形,可得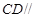
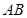 再根据线面平行的性质定理可直接证得
再根据线面平行的性质定理可直接证得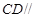 平面
平面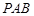 。(Ⅱ)由面面垂直的性质定理可证得
。(Ⅱ)由面面垂直的性质定理可证得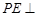 平面
平面 ,即可证得
,即可证得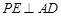 。(Ⅲ)当
。(Ⅲ)当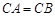 时
时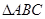 为正三角形,可得
为正三角形,可得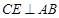 ,可根据面
,可根据面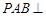 面
面 的性质定理证得
的性质定理证得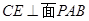 ,再根据面面垂直的判定定理可证得面
,再根据面面垂直的判定定理可证得面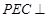 平面
平面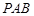 。法二
。法二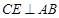 时,因为(Ⅱ)中已证
时,因为(Ⅱ)中已证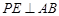 ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得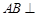 平面
平面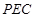 ,从而证得面
,从而证得面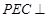 平面
平面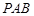
试题解析:解:(Ⅰ)因为底面
 是菱形,
是菱形,所以
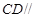
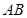 . 1分
. 1分又因为
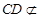 平面
平面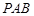 , 3分
, 3分所以
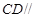 平面
平面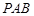 . 4分
. 4分(Ⅱ)因为
 ,点
,点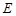 是棱
是棱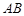 的中点,
的中点,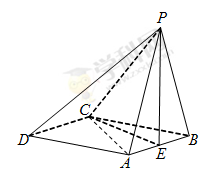
所以
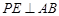 . 5分
. 5分因为平面
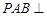 平面
平面 ,平面
,平面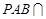 平面
平面
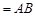 ,
,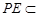 平面
平面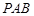 , 7分
, 7分所以
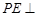 平面
平面 , 8分
, 8分因为
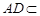 平面
平面 ,
,所以
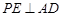 . 9分
. 9分(Ⅲ)因为
 ,点
,点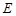 是棱
是棱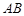 的中点,
的中点,所以
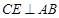 . 10分
. 10分由(Ⅱ)可得
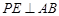 , 11分
, 11分所以
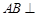 平面
平面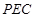 , 13分
, 13分又因为
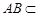 平面
平面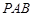 ,
,所以平面
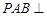 平面
平面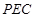 . 14分
. 14分
练习册系列答案
相关题目
 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
 平面
平面
 平面
平面 .
.

 的直角边
的直角边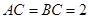 ,沿其中位线
,沿其中位线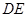 将平面
将平面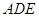 折起,使平面
折起,使平面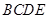 ,得到四棱锥
,得到四棱锥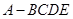 ,设
,设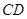 、
、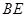 、
、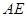 、
、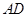 的中点分别为
的中点分别为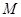 、
、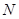 、
、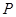 、
、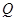 .
.


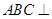 平面
平面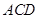 ;
;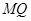 所成的角.
所成的角. 的底面
的底面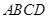 为矩形,且
为矩形,且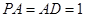 ,
,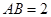 ,
,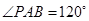 ,
,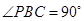 ,
,
 的棱长为
的棱长为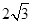 ,动点P在对角线
,动点P在对角线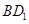 上,过点P作垂直于
上,过点P作垂直于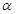 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设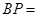 x,则当
x,则当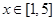 时,函数
时,函数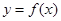 的值域为( )
的值域为( )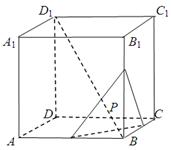
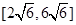
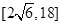
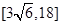
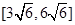
 是两条不同的直线,
是两条不同的直线,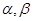 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( ) ,
,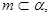
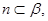 则
则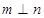
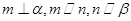 ,则
,则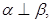
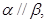
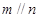
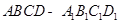 中,
中,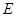 ,
,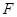 分别为棱
分别为棱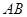 ,
,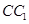 的中点,在平面
的中点,在平面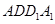 内且与平面
内且与平面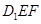 平行的直线( )
平行的直线( )