题目内容
圆心在抛物线y2=4x上且与直线x=-1相切的动圆一定经过点( )A.(0,0)
B.(1,0)
C.(0,1)
D.(2,0)
【答案】分析:由圆心在抛物线上,根据抛物线的解析式设出动圆的圆心坐标,根据直线与圆相切时圆心到直线的距离等于半径表示出圆的半径r,根据设出的圆心坐标和表示出的r写出圆的标准方程,化简后根据对应系数法即可求出x与y的值,从而得到动圆恒过定点的坐标.
解答:解:设动圆圆心坐标为( ,y),
,y),
∵动圆与直线x=-1相切,∴ -(-1)=r,即r=
-(-1)=r,即r= +1,
+1,
∴动圆的方程为: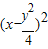 +(y-y)2=
+(y-y)2=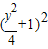 ,
,
化简得:x2+y2-1- x-2yy+
x-2yy+ =0,
=0,
即x2+y2-1=0,- x+
x+ =0,-2yy=0,
=0,-2yy=0,
解得:x=1,y=0,
则动圆恒过(1,0).
故选B
点评:本题的解题思路是设出动圆圆心坐标,表示出圆的半径r,根据圆心和半径写出圆的标准方程,从而利用对应系数法求出动圆恒过定点的坐标.要求学生掌握直线与圆相切时满足的关系,会根据圆心和半径写出圆的标准方程.其中运用对应系数法求定点坐标是解本题的关键.
解答:解:设动圆圆心坐标为(
 ,y),
,y),∵动圆与直线x=-1相切,∴
 -(-1)=r,即r=
-(-1)=r,即r= +1,
+1,∴动圆的方程为:
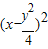 +(y-y)2=
+(y-y)2=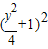 ,
,化简得:x2+y2-1-
 x-2yy+
x-2yy+ =0,
=0,即x2+y2-1=0,-
 x+
x+ =0,-2yy=0,
=0,-2yy=0,解得:x=1,y=0,
则动圆恒过(1,0).
故选B
点评:本题的解题思路是设出动圆圆心坐标,表示出圆的半径r,根据圆心和半径写出圆的标准方程,从而利用对应系数法求出动圆恒过定点的坐标.要求学生掌握直线与圆相切时满足的关系,会根据圆心和半径写出圆的标准方程.其中运用对应系数法求定点坐标是解本题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目