题目内容
(本小题满分12分)已知数列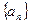 的首项为
的首项为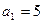 ,前
,前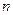 项和为
项和为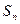 ,且
,且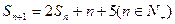
(1)求证:数列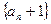 成等比数列;
成等比数列;
(2)令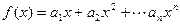 ,求函数
,求函数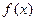 在点
在点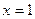 处的导数
处的导数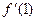 .
.
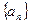 的首项为
的首项为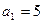 ,前
,前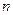 项和为
项和为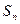 ,且
,且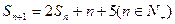
(1)求证:数列
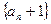 成等比数列;
成等比数列;(2)令
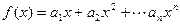 ,求函数
,求函数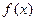 在点
在点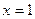 处的导数
处的导数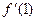 .
.(1)证明略;
(2)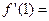
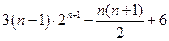
(2)
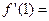
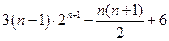
由已知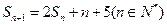 ,可得
,可得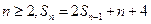 两式相减得
两式相减得
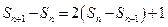 即
即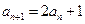 ……………………………2分
……………………………2分
从而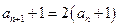 ………………………………….4分
………………………………….4分
当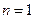 时
时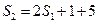 所以
所以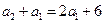 又
又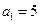 所以
所以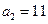
从而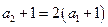
故总有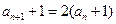 ,
,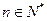 又
又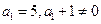
从而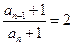 即数列
即数列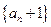 是等比数列;…………………………………5分
是等比数列;…………………………………5分
(II)由(I)知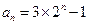 ………………………………7分
………………………………7分
因为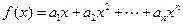 所以
所以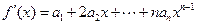
从而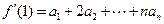 =
=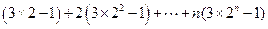
=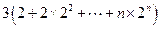 -
-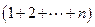 ……………………………9分
……………………………9分
=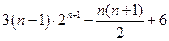 ………………………………12分
………………………………12分
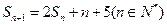 ,可得
,可得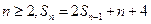 两式相减得
两式相减得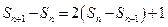 即
即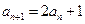 ……………………………2分
……………………………2分从而
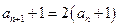 ………………………………….4分
………………………………….4分当
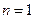 时
时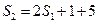 所以
所以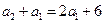 又
又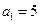 所以
所以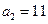
从而
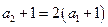
故总有
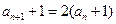 ,
,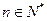 又
又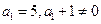
从而
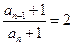 即数列
即数列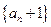 是等比数列;…………………………………5分
是等比数列;…………………………………5分(II)由(I)知
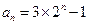 ………………………………7分
………………………………7分因为
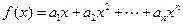 所以
所以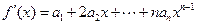
从而
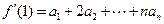 =
=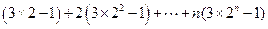
=
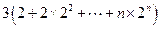 -
-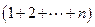 ……………………………9分
……………………………9分=
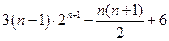 ………………………………12分
………………………………12分
练习册系列答案
相关题目
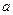 ,计划每年砍伐一些树,且每年砍伐面积的百分比
,计划每年砍伐一些树,且每年砍伐面积的百分比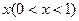 相等,当砍伐到面积的一半时,所用时间是10年。为保护生态环境,森林面
相等,当砍伐到面积的一半时,所用时间是10年。为保护生态环境,森林面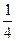 。已知到今年为止,森林剩余面积为原来的
。已知到今年为止,森林剩余面积为原来的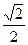 。
。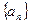 满足
满足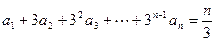
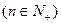
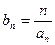 ,求数列
,求数列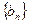 的前n项和
的前n项和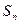 。(12分)
。(12分)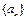 中,
中,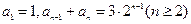 .
.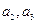 ;(2)求
;(2)求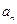 的通项公式;(3)证明:
的通项公式;(3)证明: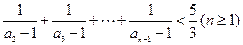
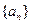 中,
中,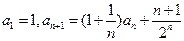
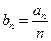 ,求数列
,求数列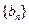 的通项公式
的通项公式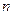 项和
项和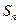
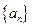 中,
中,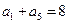 ,
,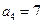 ,则
,则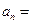 。
。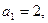
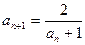 ,
,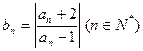 ,则数列
,则数列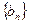 的通项公式是
的通项公式是 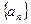 中,
中,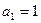 ,
,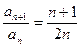 ,则其通项公式
,则其通项公式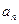 =
= 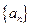 满足
满足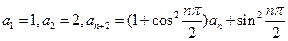 ,则该数列的前20项的和为( )
,则该数列的前20项的和为( )