题目内容
在△ABC中,已知三边长分别为a=32cm,b=23cm,c=37cm,求△ABC的面积.
解:由a=32cm,b=23cm,c=37cm,
根据余弦定理得 ,(4分)
,(4分)
又C∈(0,π),∴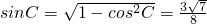 ,(8分)
,(8分)
所以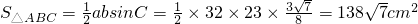 .(12分)
.(12分)
分析:由余弦定理表示出cosC,把三角形的三边代入即可求出cosC的值,由C的范围,利用同角三角函数的基本关系求出sinC的值,然后由a,b及sinC的值,利用三角形的面积公式即可求出△ABC的面积.
点评:此题考查了余弦定理,三角形的面积公式及同角三角函数间的基本关系,由三角形的三边利用余弦定理求出cosC的值,进而再利用同角三角函数间的基本关系求出sinC的值是解本题的关键.
根据余弦定理得
 ,(4分)
,(4分)又C∈(0,π),∴
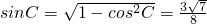 ,(8分)
,(8分)所以
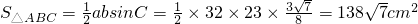 .(12分)
.(12分)分析:由余弦定理表示出cosC,把三角形的三边代入即可求出cosC的值,由C的范围,利用同角三角函数的基本关系求出sinC的值,然后由a,b及sinC的值,利用三角形的面积公式即可求出△ABC的面积.
点评:此题考查了余弦定理,三角形的面积公式及同角三角函数间的基本关系,由三角形的三边利用余弦定理求出cosC的值,进而再利用同角三角函数间的基本关系求出sinC的值是解本题的关键.

练习册系列答案
相关题目

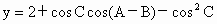 .
.