Question

在△ABC中，已知三个内角A、B、C的对边分别是a、b、c，向量

m

=（a，b），

n

=（cos（2π-B），sin（

π

2

+A）），若a≠b且

m

∥

n

，
（Ⅰ）试求内角C的大小；
（Ⅱ）若a=6，b=8，△ABC的外接圆圆心为O，点P位于劣弧

AC

上，∠PAB=60°，求四边形ABCP的面积．

Answer 1

分析：（Ⅰ）由两向量的坐标，及两向量平行，利用平面向量的数量积运算法则列出关系式，整理后求出A+B的度数，即可确定出内角C的大小；
（Ⅱ）根据题意画出图形，连接PB，利用圆周角定理得到∠APB为直角，利用30度角所对的直角边等于斜边的一半求出AP的长，再利用两角和与差的正弦函数公式求出sin∠PAC的值，利用三角形面积公式求出三角形ACP的面积，加上三角形ABC面积即可得到四边形ABCP的面积．

解答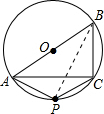：解：（Ⅰ）∵

m

=（a，b），

n

=（cos（2π-B），且

m

∥

n

，
∴bcosB-acosA=0，
利用正弦定理化简得：sinBcosB-sinAcosA=0，
即sin2A=sin2B，
∵a≠b，∴A≠B，
∴2A+2B=π，即A+B=

π

2

，
则C=

π

2

；
（Ⅱ）由题意得：BC=6，AC=8，根据勾股定理得：AB=10，
∵AB为圆的直径，∠PAB=60°，连接PB，
∴∠APB=90°，∠ABP=30°，
∴AP=

1

2

AB=5，
∵∠PAB=60°，sin∠CAB=

3

5

，cos∠CAB=

4

5

，
∴sin∠PAC=sin（60°-∠CAB）=

3

2

×

4

5

-

1

2

×

3

5

=

4 3 -3

10

，
则S_{四边形ABCP}=S_△APC+S_△ABC=

1

2

×5×8×

4 3 -3

10

+

1

2

×8×6=8

3

-6+24=8

3

+18．

点评：此题考查了正弦、余弦定理，三角形的面积公式，以及平面向量的数量积运算，熟练掌握定理及公式是解本题的关键．