题目内容
在 ABC中.
ABC中. .则A的取值范围是( )
.则A的取值范围是( )
 ABC中.
ABC中. .则A的取值范围是( )
.则A的取值范围是( ) A. (0, ] ] | B. [  , , ) ) | C. (0, ] ] | D. [  , , ) ) |
C
考点:
专题:计算题.
分析:先利用正弦定理把不等式中正弦的值转化成边,进而代入到余弦定理公式中求得cosA的范围,进而求得A的范围.
解答:解:由正弦定理可知a=2RsinA,b=2RsinB,c=2RsinC
∵sin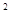 A≤sin
A≤sin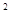 B+sin
B+sin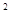 C-sinBsinC,
C-sinBsinC,
∴a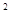 ≤b
≤b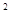 +c
+c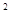 -bc
-bc
∴cosA=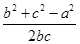 ≥
≥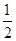
∴A≤
∵A>0
∴A的取值范围是(0, ]
]
故选C
点评:本题主要考查了正弦定理和余弦定理的应用.作为解三角形中常用的两个定理,考生应能熟练记忆.
专题:计算题.
分析:先利用正弦定理把不等式中正弦的值转化成边,进而代入到余弦定理公式中求得cosA的范围,进而求得A的范围.
解答:解:由正弦定理可知a=2RsinA,b=2RsinB,c=2RsinC
∵sin
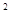 A≤sin
A≤sin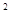 B+sin
B+sin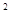 C-sinBsinC,
C-sinBsinC,∴a
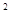 ≤b
≤b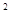 +c
+c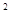 -bc
-bc∴cosA=
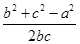 ≥
≥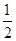
∴A≤

∵A>0
∴A的取值范围是(0,
 ]
]故选C
点评:本题主要考查了正弦定理和余弦定理的应用.作为解三角形中常用的两个定理,考生应能熟练记忆.

练习册系列答案
相关题目
 ,
, .已知
.已知 .
. ,求角A的大小;
,求角A的大小; ,求
,求 的取值范围.
的取值范围. ,已知
,已知 ,
, 的值;
的值; 的值.
的值. 中,
中, ,则
,则 ( )
( )



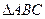 中,角
中,角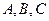 所对的边分别为
所对的边分别为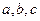 ,满足
,满足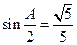 ,且
,且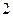 .
.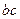 的值
的值 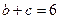 ,求
,求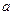 的值.
的值.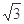 , ∠A=30°,则∠B等于 ( )
, ∠A=30°,则∠B等于 ( ) ABC中,
ABC中, 则使
则使 的范围是( )
的范围是( )



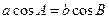 ,则这个三角形的形状是 三角形
,则这个三角形的形状是 三角形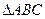 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为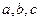 ,若
,若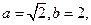
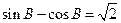 ,则角A的大小为 。
,则角A的大小为 。