题目内容
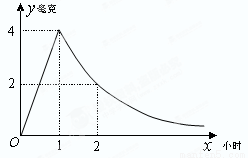
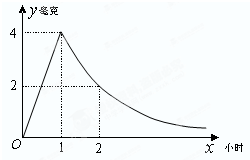 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数y=f(x)的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?
解:(1)当0≤x≤1时,y与x成正比例,设为y=kx,
又过(1,4)点,∴k=4,
∴y=4x,…
当x>1时,y=Max,又过(1,4)、(2,2)点,
∴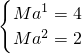 ,解得
,解得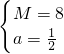 ,
,
∴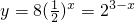 .…
.…
∴y=f(x)=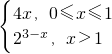 .…
.…
(2)当f(x) 时,为有效治疗,
时,为有效治疗,
当0≤x≤1时,由4x ,解得
,解得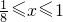 ;
;
当x>1时,23-x ,解得1<x≤4.
,解得1<x≤4.
4- =
= .
.
∴当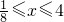 时,有治疗效果.
时,有治疗效果.
所以有效治疗时间为 小时.…
小时.…
分析:(1)当0≤x≤1时,设y=kx,又过(1,4)点,知y=4x;当x>1时,y=Max,又过(1,4)、(2,2)点,知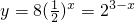 .由此能求出函数y=f(x)的解析式.
.由此能求出函数y=f(x)的解析式.
(2)当f(x) 时,为有效治疗,当0≤x≤1时,由4x
时,为有效治疗,当0≤x≤1时,由4x ,解得
,解得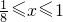 ;当x>1时,23-x
;当x>1时,23-x ,解得1<x≤4.4-
,解得1<x≤4.4- =
= .由此能求出病人一次服药后的有效治疗时间.
.由此能求出病人一次服药后的有效治疗时间.
点评:本题考查函数在生产生活中的实数据应用,解题时要认真审题,注意分析题设中的数量关系,合理地进行等价转化.
又过(1,4)点,∴k=4,
∴y=4x,…
当x>1时,y=Max,又过(1,4)、(2,2)点,
∴
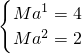 ,解得
,解得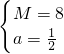 ,
,∴
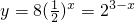 .…
.…∴y=f(x)=
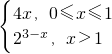 .…
.…(2)当f(x)
 时,为有效治疗,
时,为有效治疗,当0≤x≤1时,由4x
 ,解得
,解得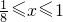 ;
;当x>1时,23-x
 ,解得1<x≤4.
,解得1<x≤4.4-
 =
= .
.∴当
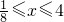 时,有治疗效果.
时,有治疗效果.所以有效治疗时间为
 小时.…
小时.…分析:(1)当0≤x≤1时,设y=kx,又过(1,4)点,知y=4x;当x>1时,y=Max,又过(1,4)、(2,2)点,知
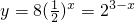 .由此能求出函数y=f(x)的解析式.
.由此能求出函数y=f(x)的解析式.(2)当f(x)
 时,为有效治疗,当0≤x≤1时,由4x
时,为有效治疗,当0≤x≤1时,由4x ,解得
,解得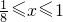 ;当x>1时,23-x
;当x>1时,23-x ,解得1<x≤4.4-
,解得1<x≤4.4- =
= .由此能求出病人一次服药后的有效治疗时间.
.由此能求出病人一次服药后的有效治疗时间.点评:本题考查函数在生产生活中的实数据应用,解题时要认真审题,注意分析题设中的数量关系,合理地进行等价转化.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
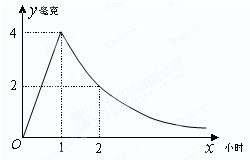 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.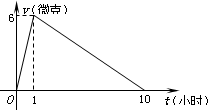 某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.
某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.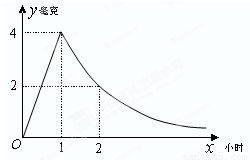
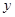 (毫克)与时间
(毫克)与时间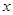 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数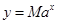 (
(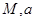 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.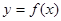 的解析式;
的解析式;