题目内容
设函数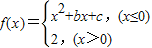
若f（-4）=f（0），f（-2）=-2，则关于x的方程f（x）=x的解的个数为 ．
【答案】分析：利用条件先求当x≤0时的函数解析式，再求x≤0时f（x）=x的解的个数；最后求当x＞0时方程f（x）=x的解为2．从而得关于x的方程f（x）=x的解的个数为3．
解答：解：当x≤0时f（x）=x2+bx+c，
因为f（-4）=f（0），f（-2）=-2，
所以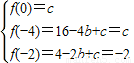
，得：b=4，c=2，
所以当x≤0时f（x）=x2+4x+2，
方程f（x）=x，即x2+3x+2=0，解得两根为：-1，-2．
当x＞0时方程f（x）=x，即x=2．
则关于x的方程f（x）=x的解的个数为 3．
故答案为：3．
点评：本题考查分段函数对应方程根的问题，需分段求解，用到了一元二次方程的解法．
解答：解：当x≤0时f（x）=x2+bx+c，
因为f（-4）=f（0），f（-2）=-2，
所以
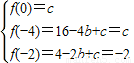，得：b=4，c=2，所以当x≤0时f（x）=x2+4x+2，
方程f（x）=x，即x2+3x+2=0，解得两根为：-1，-2．
当x＞0时方程f（x）=x，即x=2．
则关于x的方程f（x）=x的解的个数为 3．
故答案为：3．
点评：本题考查分段函数对应方程根的问题，需分段求解，用到了一元二次方程的解法．
练习册系列答案
相关题目
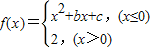若f（-4）=f（0），f（-2）=-2，则关于x的方程f（x）=x的解的个数为 ．
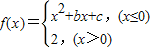若f（-4）=f（0），f（-2）=-2，则关于x的方程f（x）=x的解的个数为 ．
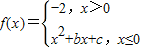若f（-4）=f（0），f（-2）=0，则关于x的不等式f（x）≤1的解集为（ ）
若f（-4）=f（0），f（-2）=0，则关于x的不等式f（x）≤1的解集为（ ）