题目内容
函数f(x)=ax2+bx+c(a≠0)的图象关于直线 对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
| A.{1,3} | B.{2,4} | C.{1,2,3,4} | D.{1,2,4,8} |
D
解析试题分析:∵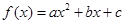 的对称轴为直线
的对称轴为直线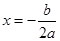 ,令设方程
,令设方程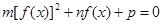 的解为
的解为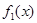 ,
, ,则必有
,则必有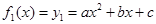 ,
,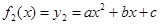 ,那么从图象上看,
,那么从图象上看,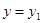 ,
,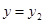 是一条平行于
是一条平行于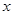 轴的直线它们与
轴的直线它们与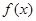 有交点,由于对称性,则方程
有交点,由于对称性,则方程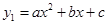 的两个解
的两个解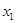 、
、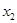 要关于直线
要关于直线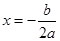 对称,也就是说
对称,也就是说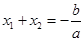 ,同理方程
,同理方程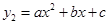 的两个解
的两个解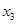 、
、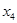 要关于直线
要关于直线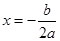 对称,那就得到
对称,那就得到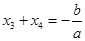 ;在C中,可以找到对称轴直线
;在C中,可以找到对称轴直线 ,也就是1,4为一个方程的解,2,3为一个方程的解,所以得到的解的集合可以是{1,2,3,4},而在D中,{1,2,4,8}找不到这样的组合使得对称轴一致,也就是说无论怎么分组,都没办法使得其中两个的和等于另外两个的和,故答案D不可能.故选D.
,也就是1,4为一个方程的解,2,3为一个方程的解,所以得到的解的集合可以是{1,2,3,4},而在D中,{1,2,4,8}找不到这样的组合使得对称轴一致,也就是说无论怎么分组,都没办法使得其中两个的和等于另外两个的和,故答案D不可能.故选D.
考点定位:二次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 ,函数
,函数 在区间
在区间 上的最大值与最小值之差为
上的最大值与最小值之差为 ,则
,则 ( )
( )
A. | B.2 | C. | D.4 |
设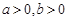 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.若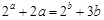 ,则 ,则 |
B.若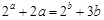 ,则 ,则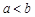 |
C.若 ,则 ,则 |
D.若 ,则 ,则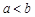 |
已知 ,
, ,则( )
,则( )
A. | B. | C. | D. |
已知 ,则下列关系中正确的是( )
,则下列关系中正确的是( )
| A.a>b>c | B.b>a>c | C.a>c>b | D.c>a>b |
函数y= 的定义域是(-∞,1)∪[2,5),则其值域是( )
的定义域是(-∞,1)∪[2,5),则其值域是( )
A.(-∞,0)∪( ,2] ,2] | B.(-∞,2] |
C.(-∞, )∪[2,+∞) )∪[2,+∞) | D.(0,+∞) |
 ________.
________. ,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是 ( )
,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是 ( )

