题目内容
设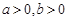 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.若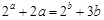 ,则 ,则 |
B.若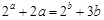 ,则 ,则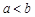 |
C.若 ,则 ,则 |
D.若 ,则 ,则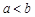 |
A
解析试题分析:对于A,B考查函数f(x)=2x+2x,g(x)=2x+3x的单调性与图象:
可知函数f(x)、g(x)在R上都单调递增,
若2a+2a=2b+3b,则a>b,因此A正确;
对于C,D分别考查函数u(x)=2x-2x,v(x)=2x-3x单调性与图象:
当 时,u′(x)<0,函数u(x)单调递减;当
时,u′(x)<0,函数u(x)单调递减;当 时,u′(x)>0,函数u(x)单调递增.
时,u′(x)>0,函数u(x)单调递增.
故在x= 取得最小值
取得最小值 .
. 当0<x<
当0<x< 时,v′(x)<0,函数v(x)单调递减;当x>
时,v′(x)<0,函数v(x)单调递减;当x> 时,v′(x)>0,函数v(x)单调递增.
时,v′(x)>0,函数v(x)单调递增.
故在x= 取得最小值
取得最小值 ,
,
据以上可画出图象.据图象可知:
当2a-2a=2b-3b,a>0,b>0时,可能a>b或a<b.因此C,D不正确.
综上可知:只有A正确.
故答案为A.
考点:用导数研究函数的单调性和图象;命题的真假判断与应用.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元部分的14%纳税;超过4 000元的按全部稿酬的11%纳税.已知某人出版一本书,共纳税420元,则这个人应得稿费(扣税前)为( ).
| A.2 800元 | B.3 000元 | C.3 800元 | D.3 818元 |
设a=40.9,b=80.48, ,则( ).
,则( ).
| A.c>a>b | B.b>a>c | C.a>b>c | D.a>c>b |
函数 的图过定点A,则A点坐标是 ( )
的图过定点A,则A点坐标是 ( )
A.( ) ) | B.( ) ) | C.(1,0) | D.(0,1) |
若 ,则
,则 +
+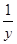 的最小值为( ).
的最小值为( ).
A. | B.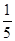 | C. | D.2 |
一轮船行驶时,单位时间的燃料费u与其速度v的立方成正比,若轮船的速度为每小时10km 时,燃料费为每小时35元,其余费用每小时为560元,这部分费用不随速度而变化.已知该轮船最高速度为25km/h, 则轮船速度为( )km/h时,轮船行每千米的费用最少.
| A.10 | B.15 | C.20 | D.25 |
函数f(x)=ax2+bx+c(a≠0)的图象关于直线 对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
| A.{1,3} | B.{2,4} | C.{1,2,3,4} | D.{1,2,4,8} |
[2014·衡阳月考]“因为指数函数y=ax是增函数(大前提),而y=( )x是指数函数(小前提),所以函数y=(
)x是指数函数(小前提),所以函数y=( )x是增函数(结论)”,上面推理的错误在于( )
)x是增函数(结论)”,上面推理的错误在于( )
| A.大前提错误导致结论错 |
| B.小前提错误导致结论错 |
| C.推理形式错误导致结论错 |
| D.大前提和小前提错误导致结论错 |
 ,函数
,函数 (
( ,求函数
,求函数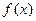 的最小值.
的最小值.