题目内容
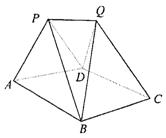
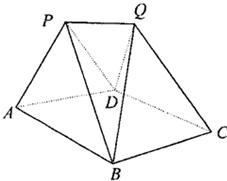 如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD,边长为1,∠BAD=60°,再在α的上侧,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD,边长为1,∠BAD=60°,再在α的上侧,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.(1)求证:PQ⊥BD;
(2)设AC与BD交于E,求cos∠PEQ;
(3)求点P到平面QBD的距离.
分析:(1)欲证PQ⊥BD,取BD中点E,连接PE、QE,只须证明BD⊥平面PQE,从而BD⊥PQ.
(2)先在三角形PEQ分别求出各边的长度,再利用余弦定理即可求得cos∠PEQ.
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,利用三棱锥的等体积变换即可求得点P到平面QBD的距离.
(2)先在三角形PEQ分别求出各边的长度,再利用余弦定理即可求得cos∠PEQ.
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,利用三棱锥的等体积变换即可求得点P到平面QBD的距离.
解答:解:(1)由P-ABD,Q-CBD是相同正三棱锥,可知△PBD与△QBD是全等等腰△.取BD中点E,连接PE、QE,则BD⊥PE,BD⊥QE.
故BD⊥平面PQE,从而BD⊥PQ.
(2)作PM⊥平面α,垂足为M,作QN⊥平面α,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=
,
PE=QE=
,PQ=MN=
,∴cos∠PEQ=
=
,
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则VP-QBD=
•S△QBD•h=
h
∴VP-QBD=
S△PEDBD=
sin∠PEQ=
=
.
∴
h=
.∴h=
.
故BD⊥平面PQE,从而BD⊥PQ.
(2)作PM⊥平面α,垂足为M,作QN⊥平面α,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=
| ||
| 6 |
PE=QE=
| 1 |
| 2 |
| ||
| 3 |
| PE2+QE2-PQ2 |
| 2PE•QE |
| 1 |
| 3 |
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则VP-QBD=
| 1 |
| 3 |
| 1 |
| 12 |
∴VP-QBD=
| 1 |
| 3 |
| 1 |
| 24 |
| 1 |
| 24 |
1-(
|
| ||
| 36 |
∴
| 1 |
| 12 |
| ||
| 36 |
| ||
| 3 |
点评:本小题主要考查异面直线所成的角、空间中直线与直线之间的位置关系、点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
 (2010•天津模拟)如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD,边长为1,∠BAD=60°,再在α的上方,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(2010•天津模拟)如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD,边长为1,∠BAD=60°,再在α的上方,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.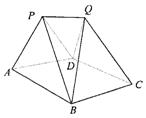

 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在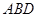 与△
与△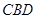 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.