题目内容
设公比大于零的等比数列{an}的前n项和为Sn,且a1=1,S4=5S2,数列{bn}的前n项和为Tn,满足b1=1, ,n∈N*.
,n∈N*.(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设Cn=(Sn+1)(nbn-λ),若数列{Cn}是单调递减数列,求实数λ的取值范围.
【答案】分析:(Ⅰ)利用a1=1,S4=5S2,求出数列的公比,即可求数列{an}的通项公式;通过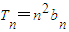 ,推出
,推出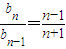 ,利用累积法求解{bn}的通项公式.
,利用累积法求解{bn}的通项公式.
(Ⅱ)求出等比数列的前n项和,化简Cn=(Sn+1)(nbn-λ),推出Cn+1-Cn,利于基本不等式求出数列{Cn}是单调递减数列,求实数λ的取值范围.
解答:(本题满分14分)
解:(Ⅰ)由S4=5S2,q>0,得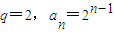 …(3分)
…(3分)
又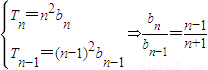 (n>1),
(n>1),
则得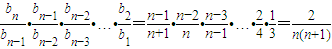
所以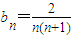 ,当n=1时也满足. …(7分)
,当n=1时也满足. …(7分)
(Ⅱ)因为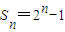 ,所以
,所以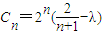 ,使数列{Cn}是单调递减数列,
,使数列{Cn}是单调递减数列,
则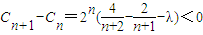 对n∈N*都成立,…(10分)
对n∈N*都成立,…(10分)
即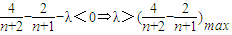 ,…(12分)
,…(12分)
 ,
,
当n=1或2时,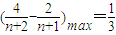 ,所以
,所以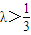 . …(14分)
. …(14分)
点评:本题考查等比数列与等差数列的综合应用,累积法的应用以及数列的函数的特征的应用,考查计算能力.
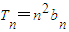 ,推出
,推出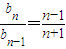 ,利用累积法求解{bn}的通项公式.
,利用累积法求解{bn}的通项公式.(Ⅱ)求出等比数列的前n项和,化简Cn=(Sn+1)(nbn-λ),推出Cn+1-Cn,利于基本不等式求出数列{Cn}是单调递减数列,求实数λ的取值范围.
解答:(本题满分14分)
解:(Ⅰ)由S4=5S2,q>0,得
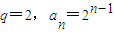 …(3分)
…(3分)又
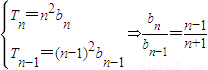 (n>1),
(n>1),则得
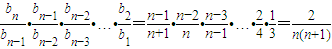
所以
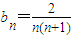 ,当n=1时也满足. …(7分)
,当n=1时也满足. …(7分)(Ⅱ)因为
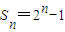 ,所以
,所以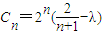 ,使数列{Cn}是单调递减数列,
,使数列{Cn}是单调递减数列,则
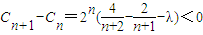 对n∈N*都成立,…(10分)
对n∈N*都成立,…(10分)即
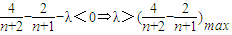 ,…(12分)
,…(12分) ,
,当n=1或2时,
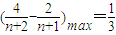 ,所以
,所以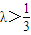 . …(14分)
. …(14分)点评:本题考查等比数列与等差数列的综合应用,累积法的应用以及数列的函数的特征的应用,考查计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 的前
的前 ,满足
,满足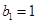 ,
, ,
, .
. 对所有的
对所有的 均成立,求实数
均成立,求实数 的取值范围.
的取值范围.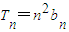 ,n∈N*.
,n∈N*.