题目内容
△ABC的三内角A,B,C所对边的长分别为a,b,c,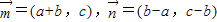 ,若
,若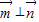 ,则sinB+sinC的取值范围是( )
,则sinB+sinC的取值范围是( )A.
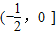
B.(
 ,
,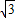 ]
]C.[
 ,1)
,1)D.[
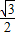 ,1)
,1)
【答案】分析:利用向量的坐标运算结合余弦定理可求得角A,从而利用两角和的正弦与辅助角公式可求sinB+sinC的取值范围.
解答:解:∵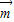 =(a+b,c),
=(a+b,c),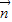 =(b-a,c-b),
=(b-a,c-b),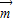 ⊥
⊥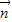 ,
,
∴(a+b)(b-a)+c(c-b)=0,
∴a2=b2+c2-bc,
由余弦定理知,a2=b2+c2-2bccosA,
∴cosA= ,而A为△ABC的内角,
,而A为△ABC的内角,
∴A=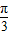 .
.
∵△ABC中,A+B+C=π,
∴B+C=π-A=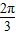 ,
,
∴sinB+sinC
=sin(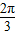 -C)+sinC
-C)+sinC
=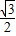 cosC-(-
cosC-(- )sinC+sinC
)sinC+sinC
= sinC+
sinC+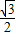 cosC
cosC
=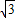 sin(C+
sin(C+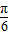 ).
).
∵0<C<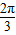 ,故
,故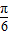 <C+
<C+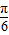 <
< .
.
∴ <sin(C+
<sin(C+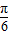 )≤1.
)≤1.
∴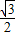 <
<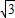 sin(C+
sin(C+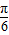 )≤
)≤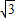 .即
.即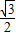 <sinB+sinC≤
<sinB+sinC≤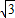 .
.
故选B.
点评:本题考查余弦定理,考查数量积判断两个平面向量的垂直关系,考查三角函数间的关系式,属于中档题.
解答:解:∵
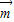 =(a+b,c),
=(a+b,c),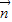 =(b-a,c-b),
=(b-a,c-b),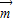 ⊥
⊥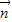 ,
,∴(a+b)(b-a)+c(c-b)=0,
∴a2=b2+c2-bc,
由余弦定理知,a2=b2+c2-2bccosA,
∴cosA=
 ,而A为△ABC的内角,
,而A为△ABC的内角,∴A=
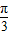 .
.∵△ABC中,A+B+C=π,
∴B+C=π-A=
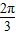 ,
,∴sinB+sinC
=sin(
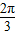 -C)+sinC
-C)+sinC=
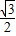 cosC-(-
cosC-(- )sinC+sinC
)sinC+sinC=
 sinC+
sinC+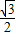 cosC
cosC=
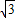 sin(C+
sin(C+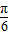 ).
).∵0<C<
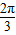 ,故
,故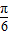 <C+
<C+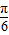 <
< .
.∴
 <sin(C+
<sin(C+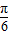 )≤1.
)≤1.∴
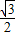 <
<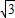 sin(C+
sin(C+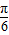 )≤
)≤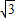 .即
.即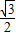 <sinB+sinC≤
<sinB+sinC≤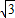 .
.故选B.
点评:本题考查余弦定理,考查数量积判断两个平面向量的垂直关系,考查三角函数间的关系式,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目