题目内容
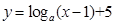 恒过定点( )
恒过定点( )A. | B.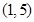  | C. | D. |
D
试题分析:因为对数函数恒过点(1,0),那么可知令x-1=1,得到
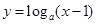 =0,即x=2,此时y=5,则说明函数
=0,即x=2,此时y=5,则说明函数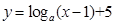 恒过点(1,5),因此答案为
恒过点(1,5),因此答案为 ,故选D.
,故选D.点评:解决该试题的关键是理解对数函数恒过定点(1,0)的真正含义,就是让对数的真数为零,无论底数是多少,则函数值始终为0。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
题目内容
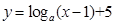 恒过定点( )
恒过定点( )A. | B.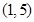  | C. | D. |
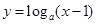 =0,即x=2,此时y=5,则说明函数
=0,即x=2,此时y=5,则说明函数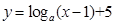 恒过点(1,5),因此答案为
恒过点(1,5),因此答案为 ,故选D.
,故选D.
 灵星计算小达人系列答案
灵星计算小达人系列答案