题目内容
已知矩形 的顶点都在半径为4的球
的顶点都在半径为4的球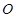 的球面上,且
的球面上,且 ,则棱锥
,则棱锥 的体积为 。
的体积为 。

解析

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
一个几何体的三视图如右图所示,则该几何体的体积为 
A. | B. | C. | D. |
题目内容
已知矩形 的顶点都在半径为4的球
的顶点都在半径为4的球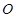 的球面上,且
的球面上,且 ,则棱锥
,则棱锥 的体积为 。
的体积为 。

解析

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案一个几何体的三视图如右图所示,则该几何体的体积为 
A. | B. | C. | D. |