题目内容
已知函数 .
.
(1)若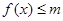 的解集为
的解集为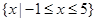 ,求实数
,求实数 的值.
的值.
(2)当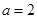 且
且 时,解关于
时,解关于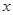 的不等式
的不等式 .
.
(1)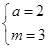 ;(2)当
;(2)当 时,原不等式的解集为
时,原不等式的解集为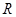 ,当
,当 时,原不等式的解集为
时,原不等式的解集为 .
.
解析试题分析:本题考查绝对值不等式的解法及利用解集求实数的值,考查学生的分类讨论思想和转化能力.第一问,利用绝对值不等式的解法求出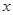 的范围,让它和已知解集相同,列出等式,解出
的范围,让它和已知解集相同,列出等式,解出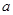 和
和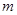 的值;第二问,先将
的值;第二问,先将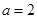 代入,得到
代入,得到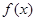 解析式,再代入到所求不等式中,找到需要解的不等式,注意到当
解析式,再代入到所求不等式中,找到需要解的不等式,注意到当 时,2个绝对值一样,所以先进行讨论,当
时,2个绝对值一样,所以先进行讨论,当 时,按照解绝对值不等式的步骤,先列出不等式组,内部求交集,综合
时,按照解绝对值不等式的步骤,先列出不等式组,内部求交集,综合 和
和 的情况得到结论.
的情况得到结论.
试题解析:(Ⅰ)由 得
得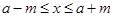 ,
,
所以 解之得
解之得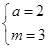 为所求. 4分
为所求. 4分
(Ⅱ)当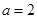 时,
时,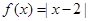 ,
,
所以
当 时,不等式①恒成立,即
时,不等式①恒成立,即 ;
;
当 时,不等式
时,不等式 或
或 或
或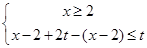 ,
,
解得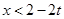 或
或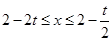 或
或 ,即
,即 ;
;
综上,当 时,原不等式的解集为
时,原不等式的解集为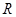 ,
,
当 时,原不等式的解集为
时,原不等式的解集为 . 10分
. 10分
考点:1.绝对值不等式的解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+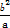 ≥a+b.
≥a+b.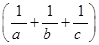 2≥6
2≥6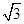 ,并确定a,b,c为何值时,等号成立.
,并确定a,b,c为何值时,等号成立.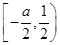 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.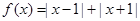 .
.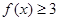 的解集;
的解集;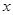 的不等式
的不等式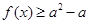 在
在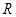 上恒成立,求实数
上恒成立,求实数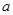 的取值范围.
的取值范围.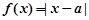 。
。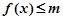 的解集为
的解集为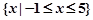 ,求实数
,求实数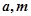 的值。
的值。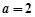 且
且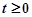 时,解关于
时,解关于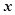 的不等式
的不等式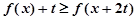 。
。 是满足下列性质的函数
是满足下列性质的函数 的全体:对于定义域B中的任何两个自变量
的全体:对于定义域B中的任何两个自变量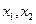 ,都有
,都有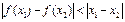 。(1)当B=R时,
。(1)当B=R时,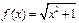 是否属于
是否属于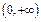 时,
时,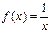 是否属于
是否属于 使
使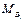 ?
?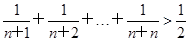 (n>1,n∈N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果是A,求代数式A.
(n>1,n∈N*)的过程中,用n=k+1时左边的代数式减去n=k时左边的代数式的结果是A,求代数式A.