题目内容
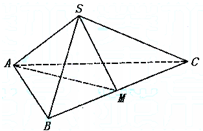
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
求:(1)
的值;
(2)二面角S-BC-A的大小;
(3)正三棱锥S-ABC的体积.
求:(1)
| AM |
| SM |
(2)二面角S-BC-A的大小;
(3)正三棱锥S-ABC的体积.

(1)∵SB=SC,AB=AC,M为BC的中点,
∴SM⊥BC,AM⊥BC.
由棱锥的侧面积等于底面积的2倍,即
3×
BC×SM=2×
BC×AM,得
=
.
(2)作正三棱锥的高SG,
则G为正三角形ABC的中心,G在AM上,GM=
AM.
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S-BC-A的平面角.
在Rt△SGM中,
∵SM=
AM=
×3GM=2GM,
∴∠SMA=∠SMG=60°,
即二面角S-BC-A的大小为60°.
(3)∵△ABC的边长是3,
∴AM=
,GM=
,SG=GMtan60°=
•
=
.
∴VS-ABC=
S△ABC•SG=
•
•
=
.

∴SM⊥BC,AM⊥BC.
由棱锥的侧面积等于底面积的2倍,即
3×
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| SM |
| 3 |
| 2 |
(2)作正三棱锥的高SG,
则G为正三角形ABC的中心,G在AM上,GM=
| 1 |
| 3 |
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S-BC-A的平面角.
在Rt△SGM中,
∵SM=
| 2 |
| 3 |
| 2 |
| 3 |
∴∠SMA=∠SMG=60°,
即二面角S-BC-A的大小为60°.
(3)∵△ABC的边长是3,
∴AM=
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∴VS-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
9
| ||
| 4 |
| 3 |
| 2 |
9
| ||
| 8 |


练习册系列答案
相关题目
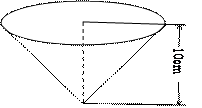
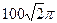

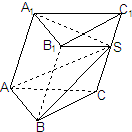

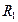 ,
,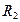 ,
,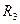 满足
满足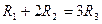 ,则它们的表面积
,则它们的表面积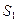 ,
,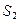 ,
,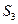 ,满足的等量关系是___________.
,满足的等量关系是___________.